Pembahasan Soal Buku Paket/BSE Matematika SMP Kelas 8 Halaman 43 (Kurikulum Merdeka) #Part 1

Berikut ini mimin sajikan pembahasan beberapa soal Buku Paket/BSE matematika SMP kelas 8 halaman 43 (kurikulum merdeka). Selamat membaca, sobat. Semoga bermanfaat.
Soal nomor 1
Selesaikan setiap sistem persamaan berikut.
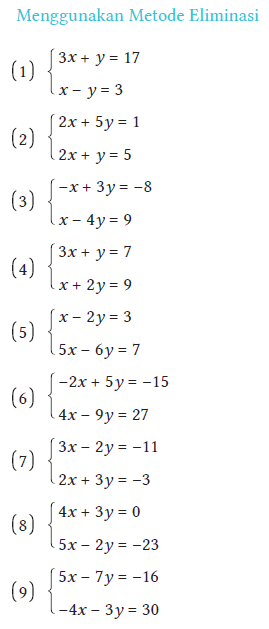
(1). $\begin{cases} &3x+y=17~~~\cdots (1)\\&x-y=3~~~\cdots (2) \end{cases}$
Penyelesaian sistem persamaannya adalah sebagai berikut
Eliminasi $y$ dari $(1)$ dan $(2)$
$ \begin{aligned} &3x+y = 17 \\ &x-y = 3 \\ & \rule{2.5 cm}{0.4pt} ~~+ \end{aligned}$
$ ~~~\color{black}{4x = 20 }$
$ ~~~ \color{black}{x =5}$
Eliminasi $x$ dari $(1)$ dan $(2)$
$\begin{aligned} \! \begin{aligned} 3x + y & = 17 \\ x-y & = 3 \end{aligned} \left| \! \begin{aligned} \times 1 \\ \times 3 \end{aligned} \right| & \! \begin{aligned}~3x+y & = 17 \\~3x-3y & = 9 \end{aligned} \\ & \rule{3 cm}{0.4pt} - \\ & \! \begin{aligned} \color{black}{4y = 8}\end{aligned} \\ & \! \begin{aligned} \color{black}{y = 2} \end{aligned} \end{aligned}$
Jadi, penyelesaian sistem persamaannya adalah
$\begin{cases} x&=5\\y&=2 \end{cases}$
(2). $\begin{cases} &2x+5y=1~~~\cdots (1)\\&2x+y=5~~~\cdots (2) \end{cases}$
Penyelesaian sistem persamaannya adalah sebagai berikut
Eliminasi $x$ dari $(1)$ dan $(2)$
$ \begin{aligned} &2x+5y = 1 \\ &2x+y = 5 \\ & \rule{2.5 cm}{0.4pt} ~~- \end{aligned}$
$ ~~~\color{black}{4y = -4 }$
$ ~~~ \color{black}{y =-1}$
Eliminasi $y$ dari $(1)$ dan $(2)$
$\begin{aligned} \! \begin{aligned} 2x + 5y & = 1 \\ 2x+y & = 5 \end{aligned} \left| \! \begin{aligned} \times 1 \\ \times 5 \end{aligned} \right| & \! \begin{aligned}~2x+5y & = 1 \\~10x+5y & = 25 \end{aligned} \\ & \rule{3 cm}{0.4pt} - \\ & \! \begin{aligned} \color{black}{-8x = -24}\end{aligned} \\ & \! \begin{aligned} \color{black}{x = 3} \end{aligned} \end{aligned}$
Jadi, penyelesaian sistem persamaannya adalah
$\begin{cases} x&=3\\y&=-1 \end{cases}$
(3). $\begin{cases} &-x+3y=-8~~~\cdots (1)\\&x-4y=9~~~\cdots (2) \end{cases}$
Penyelesaian sistem persamaannya adalah sebagai berikut
Eliminasi $x$ dari $(1)$ dan $(2)$
$ \begin{aligned} &-x+3y = -8 \\ &x-4y = 9 \\ & \rule{2.5 cm}{0.4pt} ~~+ \end{aligned}$
$ ~~~\color{black}{-y = 1 }$
$ ~~~ \color{black}{y =-1}$
Eliminasi $y$ dari $(1)$ dan $(2)$
$\begin{aligned} \! \begin{aligned} -x + 3y & = -8 \\ x-4y & = 9 \end{aligned} \left| \! \begin{aligned} \times 4 \\ \times 3 \end{aligned} \right| & \! \begin{aligned}~-4x+12y & = -32 \\~3x-12y & = 27 \end{aligned} \\ & \rule{3 cm}{0.4pt} + \\ & \! \begin{aligned} \color{black}{-x = -5}\end{aligned} \\ & \! \begin{aligned} \color{black}{x = 5} \end{aligned} \end{aligned}$
Jadi, penyelesaian sistem persamaannya adalah
$\begin{cases} x&=5\\y&=-1 \end{cases}$
(4). $\begin{cases} &3x+y=7~~~\cdots (1)\\&x+2y=9~~~\cdots (2) \end{cases}$
Penyelesaian sistem persamaannya adalah sebagai berikut
Eliminasi $x$ dari $(1)$ dan $(2)$
$\begin{aligned} \! \begin{aligned} 3x + y & = 7 \\ x+2y & = 9 \end{aligned} \left| \! \begin{aligned} \times 1 \\ \times 3 \end{aligned} \right| & \! \begin{aligned}~3x+y & = 7 \\~3x+6y & = 27 \end{aligned} \\ & \rule{2.5 cm}{0.4pt} - \\ & \! \begin{aligned} \color{black}{-5y = -20}\end{aligned} \\ & \! \begin{aligned} \color{black}{y = 4} \end{aligned} \end{aligned}$
Eliminasi $y$ dari $(1)$ dan $(2)$
$\begin{aligned} \! \begin{aligned} 3x + y & = 7 \\ x+2y & = 9 \end{aligned} \left| \! \begin{aligned} \times 2 \\ \times 1 \end{aligned} \right| & \! \begin{aligned}~6x+2y & = 14 \\~x+2y & = 9 \end{aligned} \\ & \rule{3 cm}{0.4pt} - \\ & \! \begin{aligned} \color{black}{5x = 5}\end{aligned} \\ & \! \begin{aligned} \color{black}{x = 1} \end{aligned} \end{aligned}$
Jadi, penyelesaian sistem persamaannya adalah
$\begin{cases} x&=1\\y&=4 \end{cases}$
(5). $\begin{cases} &x-2y=3~~~\cdots (1)\\&5x-6y=7~~~\cdots (2) \end{cases}$
Penyelesaian sistem persamaannya adalah sebagai berikut
Eliminasi $x$ dari $(1)$ dan $(2)$
$\begin{aligned} \! \begin{aligned} x -2 y & = 3 \\ 5x-6y & = 7 \end{aligned} \left| \! \begin{aligned} \times 5 \\ \times 1 \end{aligned} \right| & \! \begin{aligned}~5x-10y & = 15 \\~5x-6y & = 7 \end{aligned} \\ & \rule{2.5 cm}{0.4pt} - \\ & \! \begin{aligned} \color{black}{-4y = 8}\end{aligned} \\ & \! \begin{aligned} \color{black}{y = -2} \end{aligned} \end{aligned}$
Eliminasi $y$ dari $(1)$ dan $(2)$
$\begin{aligned} \! \begin{aligned} x -2 y & = 3 \\ 5x-6y & = 7 \end{aligned} \left| \! \begin{aligned} \times 3 \\ \times 1 \end{aligned} \right| & \! \begin{aligned}~3x-6y & = 9 \\~5x-6y & = 7 \end{aligned} \\ & \rule{4 cm}{0.4pt} - \\ & \! \begin{aligned} \color{black}{-2x = 2}\end{aligned} \\ & \! \begin{aligned} \color{black}{x = -1} \end{aligned} \end{aligned}$
Jadi, penyelesaian sistem persamaannya adalah
$\begin{cases} x&=-1\\y&=-2 \end{cases}$
(6). $\begin{cases} &-2x+5y=-15~~~\cdots (1)\\&4x-9y=27~~~\cdots (2) \end{cases}$
Penyelesaian sistem persamaannya adalah sebagai berikut
Eliminasi $x$ dari $(1)$ dan $(2)$
$\begin{aligned} \! \begin{aligned} -2x +5 y & = -15 \\ 4x-9y & = 27 \end{aligned} \left| \! \begin{aligned} \times 2 \\ \times 1 \end{aligned} \right| & \! \begin{aligned}~-4x+10y & = -30 \\~4x-9y & = 27 \end{aligned} \\ & \rule{2.5 cm}{0.4pt} + \\ & \! \begin{aligned} \color{black}{y = -3}\end{aligned} \end{aligned}$
Eliminasi $y$ dari $(1)$ dan $(2)$
$\begin{aligned} \! \begin{aligned} -2x +5 y & = -15 \\ 4x-9y & = 27 \end{aligned} \left| \! \begin{aligned} \times 9 \\ \times 5 \end{aligned} \right| & \! \begin{aligned}~-18x+45y & = -135 \\~20x-45y & = 135 \end{aligned} \\ & \rule{4 cm}{0.4pt} + \\ & \! \begin{aligned} \color{black}{2x = 0}\end{aligned} \\ & \! \begin{aligned} \color{black}{x = 0} \end{aligned} \end{aligned}$
Jadi, penyelesaian sistem persamaannya adalah
$\begin{cases} x&=0\\y&=-3 \end{cases}$
(7). $\begin{cases} &3x-2y=-11~~~\cdots (1)\\&2x+3y=-3~~~\cdots (2) \end{cases}$
Penyelesaian sistem persamaannya adalah sebagai berikut
Eliminasi $x$ dari $(1)$ dan $(2)$
$\begin{aligned} \! \begin{aligned} 3x -2 y & = -11 \\ 2x+3y & = -3 \end{aligned} \left| \! \begin{aligned} \times 2 \\ \times 3 \end{aligned} \right| & \! \begin{aligned}~6x-4y & = -22 \\~6x+9y & = -9 \end{aligned} \\ & \rule{2.5 cm}{0.4pt} - \\ & \! \begin{aligned} \color{black}{-13y = -13}\end{aligned} \\ & \! \begin{aligned} \color{black}{y = 1}\end{aligned} \end{aligned}$
Eliminasi $y$ dari $(1)$ dan $(2)$
$\begin{aligned} \! \begin{aligned} 3x -2 y & = -11 \\ 2x+3y & = -3 \end{aligned} \left| \! \begin{aligned} \times 3 \\ \times 2 \end{aligned} \right| & \! \begin{aligned}~9x-6y & = -33 \\~4x+6y & = -6 \end{aligned} \\ & \rule{4 cm}{0.4pt} + \\ & \! \begin{aligned} \color{black}{13x =-39 0}\end{aligned} \\ & \! \begin{aligned} \color{black}{x = -3} \end{aligned} \end{aligned}$
Jadi, penyelesaian sistem persamaannya adalah
$\begin{cases} x&=-3\\y&=1 \end{cases}$
(8). $\begin{cases} &4x+3y=0~~~\cdots (1)\\&5x-2y=-23~~~\cdots (2) \end{cases}$
Penyelesaian sistem persamaannya adalah sebagai berikut
Eliminasi $x$ dari $(1)$ dan $(2)$
$\begin{aligned} \! \begin{aligned} 4x +3 y & = 0 \\ 5x-2y & = -23 \end{aligned} \left| \! \begin{aligned} \times 5 \\ \times 4 \end{aligned} \right| & \! \begin{aligned}~20x+15y & = 0 \\~20x-8y & = -92 \end{aligned} \\ & \rule{2.5 cm}{0.4pt} - \\ & \! \begin{aligned} \color{black}{23y = 92}\end{aligned} \\ & \! \begin{aligned} \color{black}{y = 4}\end{aligned} \end{aligned}$
Eliminasi $y$ dari $(1)$ dan $(2)$
$\begin{aligned} \! \begin{aligned} 4x +3 y & = 0 \\ 5x-2y & = -23 \end{aligned} \left| \! \begin{aligned} \times 2 \\ \times 3 \end{aligned} \right| & \! \begin{aligned}~8x+6y & = 0 \\~15x-6y & = -69 \end{aligned} \\ & \rule{4 cm}{0.4pt} + \\ & \! \begin{aligned} \color{black}{23x =-69}\end{aligned} \\ & \! \begin{aligned} \color{black}{x = -3} \end{aligned} \end{aligned}$
Jadi, penyelesaian sistem persamaannya adalah
$\begin{cases} x&=-3\\y&=4 \end{cases}$
(9). $\begin{cases} &5x-7y=-16~~~\cdots (1)\\&-4x-3y=30~~~\cdots (2) \end{cases}$
Penyelesaian sistem persamaannya adalah sebagai berikut
Eliminasi $x$ dari $(1)$ dan $(2)$
$\begin{aligned} \! \begin{aligned} 5x -7 y & = -16 \\ -4x-3y & = 30 \end{aligned} \left| \! \begin{aligned} \times 4 \\ \times 5 \end{aligned} \right| & \! \begin{aligned}~20x-28y & = -64 \\~-20x-15y & = 150 \end{aligned} \\ & \rule{2.5 cm}{0.4pt} + \\ & \! \begin{aligned} \color{black}{-43y = 86}\end{aligned} \\ & \! \begin{aligned} \color{black}{y = -2}\end{aligned} \end{aligned}$
Eliminasi $y$ dari $(1)$ dan $(2)$
$\begin{aligned} \! \begin{aligned} 5x -7 y & = -16 \\ -4x-3y & = 30 \end{aligned} \left| \! \begin{aligned} \times 3 \\ \times 7 \end{aligned} \right| & \! \begin{aligned}~15x-21y & = -48 \\~-28x-21y & = 210 \end{aligned} \\ & \rule{4 cm}{0.4pt} - \\ & \! \begin{aligned} \color{black}{43x =-258}\end{aligned} \\ & \! \begin{aligned} \color{black}{x = -6} \end{aligned} \end{aligned}$
Jadi, penyelesaian sistem persamaannya adalah
$\begin{cases} x&=-6\\y&=-2 \end{cases}$
Demikianlah pembahasan beberapa soal Buku Paket/BSE matematika SMP kelas 8 halaman 43 (kurikulum merdeka). Semoga bermanfaat.
Referensi
Tim Gakko Tosho. 2021. Matematika untuk Sekolah Menengah Pertama Kelas VIII . Jakarta: Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi.