Cara Menentukan Minor dan Kofaktor Matriks Ordo 3x3

Berikut ini mimin sajikan cara menentukan minor dan kofaktor matriks ordo 3x3. Selamat membaca, sobat. Semoga bermanfaat.
Minor
Misalkan matriks $A = \begin{pmatrix}a_{11} & a_{12} & a_{13}\\a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\end{pmatrix}$
Minor elemen $a_{ij}$ dinotasikan dengan $M_{ij}$ adalah determinan dari matriks baru ordo 2x2 yang diperoleh setelah elemen-elemen pada baris ke-$i$ dan kolom ke-$j$ dihilangkan.
$\bullet$ Misal akan dicari $M_{11}$, maka kita hilangkan elemen-elemen baris ke-$1$ dan kolom ke-$1$ seperti berikut

Sehingga diperoleh $M_{11}=\begin{vmatrix} a_{22} & a_{23}\\ a_{32} & a_{33} \end{vmatrix}$
Untuk selanjutnya, kita dapat mencari minor yang lain dengan cara yang serupa seperti diatas.
$\bullet ~M_{12}$ (hilangkan elemen-elemen baris ke-$1$ dan kolom ke-$2$)

Sehingga diperoleh $M_{12}=\begin{vmatrix} a_{21} & a_{23}\\ a_{31} & a_{33} \end{vmatrix}$
$\bullet ~M_{13}$ (hilangkan elemen-elemen baris ke-$1$ dan kolom ke-$3$)

Sehingga diperoleh $M_{13}=\begin{vmatrix} a_{21} & a_{22}\\ a_{31} & a_{32} \end{vmatrix}$
$\bullet~M_{21}$ (hilangkan elemen-elemen baris ke-$2$ dan kolom ke-$1$)

Sehingga diperoleh $M_{21}=\begin{vmatrix} a_{12} & a_{13}\\ a_{32} & a_{32} \end{vmatrix}$
$\bullet~M_{22}$ (hilangkan elemen-elemen baris ke-$2$ dan kolom ke-$2$)

Sehingga diperoleh $M_{22}=\begin{vmatrix} a_{11} & a_{13}\\ a_{31} & a_{33} \end{vmatrix}$
$\bullet~M_{23}$ (hilangkan elemen-elemen baris ke-$2$ dan kolom ke-$3$)

Sehingga diperoleh $M_{23}=\begin{vmatrix} a_{11} & a_{12}\\ a_{31} & a_{32} \end{vmatrix}$
$\bullet~M_{31}$ (hilangkan elemen-elemen baris ke-$3$ dan kolom ke-$1$)

Sehingga diperoleh $M_{31}=\begin{vmatrix} a_{12} & a_{13}\\ a_{22} & a_{23} \end{vmatrix}$
$\bullet~M_{32}$ (hilangkan elemen-elemen baris ke-$3$ dan kolom ke-$2$)

Sehingga diperoleh $M_{32}=\begin{vmatrix} a_{11} & a_{13}\\ a_{21} & a_{23} \end{vmatrix}$
$\bullet~M_{33}$ (hilangkan elemen-elemen baris ke-$3$ dan kolom ke-$3$)
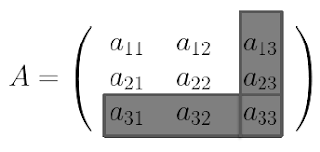
Sehingga diperoleh $M_{33}=\begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix}$
Kofaktor
Kofaktor elemen $a_{ij}$ dinotasikan dengan $K_{ij}$ adalah hasil kali $(-1)^{i+j}$ dengan minor elemen tersebut. Sehingga didapat rumus untuk mencari kofaktor sebagai berikut.
$K_{ij}=(-1)^{i+j} ~ M_{ij} $
Ket :
$K_{ij}$ merupakan kofaktor elemen $a_{ij}$
$M_{ij}$ merupakan minor elemen $a_{ij}$
Dari matriks $A = \begin{pmatrix}a_{11} & a_{12} & a_{13}\\a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\end{pmatrix}$, dapat diperoleh kofaktor-kofaktor sebagai berikut.
$K_{11}=(-1)^{1+1} ~ M_{11}= M_{11} $
$K_{12}=(-1)^{1+2} ~ M_{12}= -M_{12} $
$K_{13}=(-1)^{1+3} ~ M_{13}= M_{13}$
$K_{21}=(-1)^{2+1} ~ M_{21}= -M_{21}$
$K_{22}=(-1)^{2+2} ~ M_{22}= M_{22}$
$K_{23}=(-1)^{2+3} ~ M_{23}= -M_{23}$
$K_{31}=(-1)^{3+1} ~ M_{31}= M_{31}$
$K_{32}=(-1)^{3+2} ~ M_{32}= -M_{32}$
$K_{33}=(-1)^{3+3} ~ M_{33}= M_{33}$
Sehingga didapat kofaktor matriks $A$ sebagai berikut.
$\begin{aligned} kof~(A) &= \begin{pmatrix}K_{11} & K_{12} & K_{13}\\K_{21} & K_{22} & K_{23}\\ K_{31} & K_{32} & K_{33}\end{pmatrix}\\ \\ &= \begin{pmatrix}M_{11} & -M_{12} & M_{13}\\-M_{21} & M_{22} & -M_{23}\\ M_{31} & -M_{32} & M_{33}\end{pmatrix} \end{aligned}$
Untuk lebih jelasnya, berikut ini contoh soal menentukan minor dan kofaktor matriks ordo 3x3
Contoh soal
Diketahui $B = \begin{pmatrix}~1 & 2 & 3~\\ ~2 & 5 & 3~\\~1 & 0 & 8~\end{pmatrix}$, maka $kof~(B) $ adalah ...
Jawab:
$K_{11}=(-1)^{1+1} ~ \begin{vmatrix} 5 & 3\\ 0 & 8 \end{vmatrix}= 40-0=40 $
$K_{12}=(-1)^{1+2} ~ \begin{vmatrix} 2 & 3\\ 1 & 8 \end{vmatrix}= -(16-3)=-13 $
$K_{13}=(-1)^{1+3} ~ \begin{vmatrix} 2 & 5\\ 1 & 0 \end{vmatrix}= 0-5=-5$
$K_{21}=(-1)^{2+1} ~ \begin{vmatrix} 2 & 3\\ 0 & 8 \end{vmatrix}= -(16-0)=-16$
$K_{22}=(-1)^{2+2} ~ \begin{vmatrix} 1 & 3\\ 1 & 8 \end{vmatrix}= 8-3=5$
$K_{23}=(-1)^{2+3} ~ \begin{vmatrix} 1 & 2\\ 1 & 0 \end{vmatrix}= -(0-2)=2$
$K_{31}=(-1)^{3+1} ~ \begin{vmatrix} 2 & 3\\ 5 & 3 \end{vmatrix}= 6-15=-9$
$K_{32}=(-1)^{3+2} ~ \begin{vmatrix} 1 & 3\\ 2 & 3 \end{vmatrix}= -(3-6)=3$
$K_{33}=(-1)^{3+3} ~ \begin{vmatrix} 1 & 2\\ 2 & 5 \end{vmatrix}= 5-4=1$
Jadi, $kof~(B) = \begin{pmatrix}40 & -13 & -5\\-16 & 5 & 2\\ -9 & 3 & 1\end{pmatrix}$
Demikianlah ulasan terkait cara menentukan minor dan kofaktor matriks ordo 3x3. Semoga bermanfaat.
Referensi:
E. S., Pesta dan Cecep Anwar H. F. S. 2008. Matematika aplikasi : untuk SMA dan MA kelas XII program studi ilmu alam. Jakarta: Pusat Perbukuan Departemen Pendidikan Nasional.
Y., Rosihan Ari dan Indriyastuti. 2009. Khasanah Matematika 3: untuk kelas XII SMA/MA Program Bahasa. Jakarta: Pusat Perbukuan Departemen Pendidikan Nasional.