Contoh Soal Persamaan Lingkaran beserta Pembahasannya

Definisi
Lingkaran adalah tempat kedudukan titik-titik yang berjarak sama terhadap satu titik tertentu. Titik tertentu tersebut disebut dengan pusat lingkaran dan jarak yang sama antara pusat lingkaran dengan setiap titik disebut dengan jari-jari lingkaran.
Persamaan Lingkaran Berpusat di O(0,0) dan Berjari-jari r
Persamaan lingkaran yang berpusat di $O(0,0)$ dan berjari-jari $r$ adalah $\boxed{x^{2}+y^{2}=r^{2}}$
Persamaan Lingkaran dengan Pusat P(a,b) dan Berjari-jari r
Persamaan lingkaran yang berpusat di $P(a,b)$ dan berjari-jari $r$ adalah $\boxed{(x-a)^{2}+(y-b)^{2}=r^{2}}$
Bentuk Umum Persamaan Lingkaran
Jika rumus persamaan lingkaran yang berpusat di $P(a,b)$ dan berjari-jari $r$ dijabarkan, maka dapat diperoleh bentuk berikut
$\begin{aligned} (x-a)^2 + (y-b)^2 & = r^2 \\ (x^2 - 2ax + a^2) + (y^2 - 2by + b^2) & = r^2 \\ x^2 + y^2 - 2ax - 2by + (a^2 + b^2 - r^2) & = 0 \end{aligned}$
Bentuk terakhir yang diperoleh diatas adalah sama dengan
$\boxed{x^2 + y^2 + Ax + By + C = 0}$
dengan
$A=-2a$;
$B=-2b$; dan
$C= (a^2 + b^2 - r^2)$; $A$,$B$, dan $C$ bilangan real
Jadi, $x^2 + y^2 + Ax + By + C = 0$ merupakan bentuk umum persamaan lingkaran. Jika bentuk umum persamaan lingkaran ini diubah dalam bentuk kuadrat sempurna maka dapat diperoleh pusat dan jari-jari lingkaran.
$\begin{aligned} x^2 + y^2 + Ax + By + C &= 0\\ (x^2+ Ax) + (y^2 + By) &= -C\\ (x^2+ Ax+(\frac{1}{2}A)^{2}) + (y^2 + By+(\frac{1}{2}B)^{2}) &=(\frac{1}{2}A)^{2}+(\frac{1}{2}B)^{2} -C\\ (x+\frac{1}{2}A)^{2}+(x+\frac{1}{2}B)^{2}&=\frac{1}{4}A^{2}+\frac{1}{4}B^{2} -C \end{aligned}$
Sehingga diperoleh
$\text{Pusat lingkaran :}\ P(-\frac{1}{2}A,-\frac{1}{2}B)$ dan
$\begin{aligned} \text{Jari-jari lingkaran :}\ r^{2}&=\frac{1}{4}A^{2}+\frac{1}{4}B^{2} -C \\ r&=\sqrt{\frac{1}{4}A^{2}+\frac{1}{4}B^{2} -C} \end{aligned}$
Berikut ini beberapa contoh soal persamaan lingkaran beserta pembahasannya.
Contoh soal 1
Tentukan persamaan lingkaran yang berpusat di titik $O(0,0)$ dengan panjang jari-jari $4 \sqrt{3}$.
Jawab:
Diketahui jari-jari $r=4 \sqrt{3}$ sehingga $r^{2}=(4 \sqrt{3})^{2}=48$
Persamaan lingkaran yang berpusat di $O(0,0)$ dan berjari-jari $r$ adalah $x^{2}+y^{2}=r^{2}$
Jadi, persamaan lingkarannya adalah
$ \boxed{x^{2}+y^{2} = 48}$
Contoh soal 2
Tentukan persamaan lingkaran yang berpusat di titik $O(0,0)$ dan melalui titik $(-12,5)$.
Jawab:
Persamaan lingkaran yang berpusat di $O(0,0)$ dan berjari-jari $r$ adalah $x^{2}+y^{2}=r^{2}$
Karena lingkaran melalui titik $(-12,5)$, maka dengan menyubstitusikan titik $(-12,5)$ pada pers. $x^{2}+y^{2}=r^{2}$ diperoleh
$\begin{aligned} x^{2}+y^{2} &= r^{2} \\ (-12)^{2}+5^{2} &= r^{2} \\ 144+25 &= r^{2} \\ 169 &= r^{2} \end{aligned}$
Jadi, persamaan lingkarannya adalah
$ x^{2}+y^{2} = r^{2}$
$ \boxed{x^{2}+y^{2} = 169 }$
Contoh soal 3
Tentukan persamaan lingkaran yang berpusat di titik $P(3,-4)$ dengan jari-jari $2$.
Jawab:
Persamaan lingkaran yang berpusat di $P(a,b)$ dan berjari-jari $r$ adalah $(x-a)^{2}+(y-b)^{2}=r^{2}$
Untuk pusat $P(3,-4)$ dengan jari-jari $2$, diperoleh
$\begin{aligned} (x-a)^{2}+(y-b)^{2} &= r^{2} \\ (x-3)^{2}+(y-(-4))^{2} &= 2^{2} \\ (x-3)^{2}+(y+4)^{2} &= 4 \end{aligned}$
Jadi, persamaan lingkarannya adalah $\boxed{(x-3)^{2}+(y+4)^{2} = 4}$
Contoh soal 4
Tentukan persamaan lingkaran yang berpusat di titik $P(4,-3)$ dan menyinggung sumbu $Y$
Jawab:

Dari ilustrasi gambar diatas dapat diketahui bahwa dengan pusat lingkaran di titik $P(4,-3)$ maka panjang jari-jarinya adalah $4$ (karena lingkaran menyinggung sumbu Y)
Sehingga diperoleh persamaan lingkaran
$\begin{aligned} (x-a)^{2}+(y-b)^{2} &= r^{2} \\ (x-4)^{2}+(y-(-3))^{2} &= 4^{2} \\ (x-4)^{2}+(y+3)^{2} &= 16 \end{aligned}$
Jadi, persamaan lingkarannya adalah $\boxed{(x-4)^{2}+(y+3)^{2} = 16}$
Contoh soal 5
Tentukan persamaan lingkaran yang berpusat di titik $P(3,4)$ dan menyinggung sumbu $X$
Jawab:
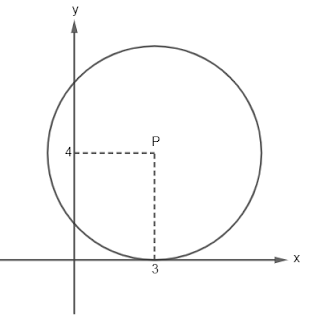
Dari ilustrasi gambar diatas dapat diketahui bahwa dengan pusat lingkaran di titik $P(3,4)$ maka panjang jari-jarinya adalah $4$ (karena lingkaran menyinggung sumbu X)
Sehingga diperoleh persamaan lingkaran
$\begin{aligned} (x-a)^{2}+(y-b)^{2} &= r^{2} \\ (x-3)^{2}+(y-4)^{2} &= 4^{2} \\ (x-3)^{2}+(y-4)^{2} &= 16 \end{aligned}$
Jadi, persamaan lingkarannya adalah $\boxed{(x-3)^{2}+(y-4)^{2} = 16}$
Contoh soal 6
Tentukan pusat dan jari-jari lingkaran $x^2 + y^2 + 6x -4y -3 = 0$
Jawab:
Bentuk umum persamaan lingkaran adalah $x^2 + y^2 + Ax + By + C = 0$. Dengan demikian $A=6$, $B=-4$, dan $C=-3$
Sehingga diperoleh
$ \text{Pusat lingkaran :}\ P(-\frac{1}{2}A,-\frac{1}{2}B)=P(-3,2)$
$\begin{aligned} \text{Jari-jari lingkaran :}\ r&=\sqrt{\frac{1}{4}A^{2}+\frac{1}{4}B^{2} -C} \\ &= \sqrt{\frac{1}{4}.36+\frac{1}{4}.16 +3}\\ &= \sqrt{16} \\ &=4 \end{aligned}$
Jadi, pusat lingkarannya adalah $P(-3,2)$ dengan jari-jari $r=4$
Contoh soal 7
Tentukan persamaan lingkaran yang berpusat di titik $P(3,4)$ dan melalui titik $Q(5,6)$
Jawab:
Rumus jarak antara titik $P(x_1,y_1)$ dan $Q(x_2,y_2)$ adalah $PQ=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}$
Jarak antara titik $P(3,4)$ dan titik $Q(5,6)$ adalah jari-jari lingkaran, yaitu
$\begin{aligned} r &=\sqrt{(5-3)^{2}+(6-4)^{2}} \\ &= \sqrt{(2)^{2}+(2)^{2}} \\ &= \sqrt{8} \end{aligned}$
Sehingga diperoleh persamaan lingkaran
$\begin{aligned} (x-a)^{2}+(y-b)^{2} &= r^{2} \\ (x-3)^{2}+(y-4)^{2} &= (\sqrt{8})^{2} \\ (x-3)^{2}+(y-4)^{2} &= 8 \end{aligned}$
Jadi, persamaan lingkarannya adalah $\boxed{(x-3)^{2}+(y-4)^{2} = 8}$
Contoh soal 8
Tentukan persamaan lingkaran yang berpusat di titik $P(6,5)$ dan menyinggung garis $y=1$
Jawab:
Rumus jarak dari titik $P(x_1,y_1)$ ke garis $ax+by+c=0$ adalah
$\begin{align} d = \left| \frac{a.x_1 + b.y_1 + c}{\sqrt{a^2 + b^2}} \right| \end{align}$
Jarak dari pusat $P(6,5)$ ke garis $y=1$ adalah jari-jari lingkaran, yaitu
$\begin{align} r &= \left| \frac{0.6 + 1.5 + (-1)}{\sqrt{0^2 + 1^2}} \right| \\ &= \left| \frac{4}{1} \right| \\ &= 4 \end{align}$
Sehingga diperoleh persamaan lingkaran
$\begin{aligned} (x-a)^{2}+(y-b)^{2} &= r^{2} \\ (x-6)^{2}+(y-5)^{2} &= (4)^{2} \\ (x-6)^{2}+(y-5)^{2} &= 16 \end{aligned}$
Jadi, persamaan lingkarannya adalah $\boxed{(x-6)^{2}+(y-5)^{2} = 16}$
Contoh soal 9
Tentukan persamaan lingkaran dari gambar di bawah ini

Jawab:
Bentuk umum persamaan lingkaran adalah $x^2 + y^2 + Ax + By + C = 0$
Substitusi titik $P,Q,$ dan $R$ ke bentuk umum persamaan lingkaran
$\bullet$ untuk titik $P(2,-2)$
$\begin{aligned} x^2 + y^2 + Ax + By + C &= 0 \\ 2^2 + (-2)^2 + A.2 + B.(-2) + C &= 0 \\ 8 + 2A-2B + C &= 0\\ 2A-2B + C &= -8\ ...(1) \end{aligned}$
$\bullet$ untuk titik $Q(7,3)$
$\begin{aligned} x^2 + y^2 + Ax + By + C &= 0 \\ 7^2 + 3^2 + A.7 + B.3 + C &= 0 \\ 58 + 7A+3B + C &= 0\\ 7A +3B+ C &= -58\ ...(2) \end{aligned}$
$\bullet$ untuk titik $R(6,4)$
$\begin{aligned} x^2 + y^2 + Ax + By + C &= 0 \\ 6^2 + 4^2 + A.6 + B.4 + C &= 0 \\ 52 + 6A+4B + C &= 0\\ 6A+4B + C &= -52\ ...(3) \end{aligned}$
Sehingga didapat 3 persamaan yaitu
$2A-2B + C = -8\ ...(1)$
$7A +3B+ C = -58\ ...(2)$
$6A+4B + C = -52\ ...(3)$
Kita selesaikan ketiga persamaan tersebut untuk memperoleh nilai A, B, dan C
Eliminasi C dari (1) dan (2)
$\begin{aligned} 2A-2B + C &= -8 \\ 7A +3B+ C &= -58\ -\\ \hline \\ -5A-5B&= 50\ ...(4) \end{aligned}$
Eliminasi C dari (2) dan (3)
$\begin{aligned} 7A +3B+ C &= -58 \\ 6A+4B + C &= -52\ -\\ \hline \\ A-B&= -6\ ...(5) \end{aligned}$
Eliminasi $B$ dari $(4)$ dan $(5)$
$\begin{aligned} \! \begin{aligned} -5A-5B&= 50 \\ A-B&= -6 \end{aligned} \left| \! \begin{aligned} \times 1 \\ \times 5 \end{aligned} \right| & \! \begin{aligned}~-5A-5B&= 50 \\~5A-5B&= -30 \end{aligned} \\ & \rule{5.5 cm}{0.4pt} - \\ & \! \begin{aligned} \color{black}{-10A =80 } \end{aligned} \\ & \! \begin{aligned} \color{black}{~~~~~~~A = -8} \end{aligned} \end{aligned}$
Substitusi $A = -8$ ke $(5)$
$A-B= -6$
$ \Leftrightarrow -8-B= -6$
$ \Leftrightarrow B= -2$
Substitusi $A = -8$ dan $B= -2$ ke $(1)$
$2A-2B + C = -8$
$ \Leftrightarrow 2(-8)-2(-2) + C = -8$
$ \Leftrightarrow -16+4 + C = -8$
$ \Leftrightarrow C = 4$
Jadi, persamaan lingkarannya adalah
$x^2 + y^2 + Ax + By + C = 0$
$\boxed{x^2 + y^2 -8x -2y + 4 = 0}$
Demikianlah beberapa contoh soal dan pembahasan pada materi persamaan lingkaran. Semoga bermanfaat.
Referensi:
Djumanta, Wahyudin dan R. Sudrajat. 2008. Mahir Mengembangkan Matematika 2:untuk Kelas XI mengengah Atas / Madrasah Aliyah. Jakarta: Pusat Perbukuan Departemen Pendidikan Nasional.
Kementerian Pendidikan dan Kebudayaan. 2014. Matematika untuk SMA/MA/SMK/MAK Kelas XI Semester 2. Jakarta: Kementerian Pendidikan dan Kebudayaan.