Contoh Soal Transformasi Geometri - Rotasi beserta Pembahasannya
Rotasi
Rotasi (perputaran) merupakan transformasi yang memutar suatu objek melalui suatu pusat dan sudut tertentu.
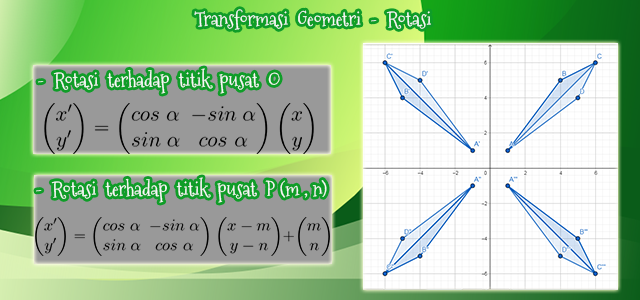
$\bullet$ Jika titik $A(x,y)$ dirotasikan sebesar $\alpha$ dengan titik pusat $O(0,0)$, maka akan diperoleh :
$\begin{pmatrix} x' \\ y'\end{pmatrix} = \begin{pmatrix} cos\ \alpha & -sin\ \alpha \\ sin\ \alpha & cos\ \alpha \end{pmatrix}\begin{pmatrix} x \\ y\end{pmatrix}$
$\bullet$ Jika titik $A(x,y)$ dirotasikan sebesar $\alpha$ dengan titik pusat $P(m,n)$, maka akan diperoleh :
$\begin{pmatrix} x' \\ y'\end{pmatrix} = \begin{pmatrix} cos\ \alpha & -sin\ \alpha \\ sin\ \alpha & cos \ \alpha \end{pmatrix}\begin{pmatrix} x - m \\ y - n\end{pmatrix} + \begin{pmatrix} m \\ n\end{pmatrix}$
$\bullet$ Jika titik $A(x,y)$ dirotasikan sebesar $\alpha$ dengan titik pusat $O(0,0)$. Kemudian dirotasi lagi sebesar $\beta$ dengan pusat yang sama, maka akan diperoleh :
$\begin{pmatrix} x'' \\ y''\end{pmatrix} = \begin{pmatrix} cos\ (\alpha+\beta) & -sin\ (\alpha+\beta) \\ sin\ (\alpha+\beta) & cos\ (\alpha+\beta) \end{pmatrix}\begin{pmatrix} x \\ y\end{pmatrix}$
$\bullet$ Jika titik $A(x,y)$ dirotasikan sebesar $\alpha$ dengan titik pusat $P(m,n)$. Kemudian dirotasi lagi sebesar $\beta$ dengan pusat yang sama, maka akan diperoleh :
$\begin{pmatrix} x'' \\ y''\end{pmatrix} = \begin{pmatrix} cos\ (\alpha+\beta) & -sin\ (\alpha+\beta) \\ sin\ (\alpha+\beta) & cos\ (\alpha+\beta) \end{pmatrix}\begin{pmatrix} x-m \\ y-n\end{pmatrix} + \begin{pmatrix} m \\ n\end{pmatrix}$
Berikut ini beberapa contoh soal transformasi rotasi dan pembahasannya.
Contoh soal 1
Tentukanlah bayangan titik $V(5,2)$ yang dirotasi $30^\circ$ berlawanan dengan arah perputaran jarum jam dengan pusat putar $O(0,0)$
Jawab:
Diketahui : Titik $V(5,2)$ dirotasi sebesar $\alpha=30^\circ$ dengan pusat $O(0,0)$
$\begin{aligned} \left( \begin{matrix} x' \\ y' \end{matrix} \right) & = \left(\begin{matrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{matrix} \right) \left( \begin{matrix} x \\ y \end{matrix} \right) \\ \\ & = \left( \begin{matrix} \cos 30^\circ & -\sin 30^\circ \\ \sin 30^\circ & \cos 30^\circ \end{matrix} \right) \left( \begin{matrix} 5 \\ 2 \end{matrix} \right) \\ \\ & = \left( \begin{matrix} \frac{1}{2}\sqrt{3} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2}\sqrt{3} \end{matrix} \right) \left( \begin{matrix} 5 \\ 2 \end{matrix} \right) \\ \\ & = \left( \begin{matrix} \frac{5}{2}\sqrt{3} -1 \\ \frac{5}{2} + \sqrt{3} \end{matrix} \right) \end{aligned}$
Jadi, bayangan titik $V$ adalah $V'(\frac{5}{2}\sqrt{3} -1, \frac{5}{2} + \sqrt{3} )$
Contoh soal 2
Tentukanlah bayangan titik $W(4,12)$ yang dirotasi $90^\circ$ searah dengan arah perputaran jarum jam dengan pusat putar $A(2,2)$
Jawab:
Diketahui : Titik $W(4,12)$ dirotasi sebesar $\alpha=\color{red}{-90^\circ}$(karena searah dengan arah perputaran jarum jam) dengan pusat $A(2,2)$
$\begin{aligned} \begin{pmatrix} x' \\ y'\end{pmatrix} &= \begin{pmatrix} cos\ \alpha & -sin\ \alpha \\ sin\ \alpha & cos \ \alpha \end{pmatrix}\begin{pmatrix} x - m \\ y - n\end{pmatrix} + \begin{pmatrix} m \\ n\end{pmatrix} \\ \\ &= \begin{pmatrix} cos\ (-90^\circ) & -sin\ (-90^\circ) \\ sin\ (-90^\circ) & cos \ (-90^\circ) \end{pmatrix}\begin{pmatrix} 4 - 2 \\ 12 - 2\end{pmatrix} + \begin{pmatrix} 2 \\ 2\end{pmatrix} \\ \\ &= \begin{pmatrix} cos\ 90^\circ & sin\ 90^\circ \\ -sin\ 90^\circ & cos \ 90^\circ \end{pmatrix}\begin{pmatrix} 2 \\ 10 \end{pmatrix} + \begin{pmatrix} 2 \\ 2\end{pmatrix} \\ \\ &= \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}\begin{pmatrix} 2 \\ 10 \end{pmatrix} + \begin{pmatrix} 2 \\ 2\end{pmatrix} \\ \\ &= \begin{pmatrix} 10 \\ -2 \end{pmatrix} + \begin{pmatrix} 2 \\ 2\end{pmatrix} \\ \\ &= \begin{pmatrix} 12 \\ 0 \end{pmatrix} \end{aligned}$
Note: $\cos ( - \alpha ) = \cos \alpha$, $\sin (- \alpha ) = - \sin \alpha$
Jadi, bayangan titik $W$ adalah $W'(12,0 )$
Contoh soal 3
Tentukanlah bayangan titik $X(3,-4)$ yang dirotasi $90^\circ$ berlawanan dengan arah perputaran jarum jam dengan pusat putar $O(0,0)$. Kemudian, dilanjutkan dengan rotasi $30^\circ$ dengan arah dan pusat yang sama.
Jawab:
Diketahui : Titik $X(3,-4)$ dirotasi sebesar $(\alpha+\beta)=90^\circ+30^\circ=120^\circ$ dengan pusat $O(0,0)$
$\begin{aligned} \begin{pmatrix} x'' \\ y''\end{pmatrix} &= \begin{pmatrix} cos\ (\alpha+\beta) & -sin\ (\alpha+\beta) \\ sin\ (\alpha+\beta) & cos\ (\alpha+\beta) \end{pmatrix}\begin{pmatrix} x \\ y\end{pmatrix} \\ \\ &= \begin{pmatrix} cos\ 120^\circ & -sin\ 120^\circ \\ sin\ 120^\circ & cos\ 120^\circ \end{pmatrix}\begin{pmatrix} 3 \\ -4 \end{pmatrix} \\ \\ &= \begin{pmatrix} -\frac{1}{2} & -\frac{1}{2}\sqrt{3} \\ \frac{1}{2}\sqrt{3} & -\frac{1}{2} \end{pmatrix}\begin{pmatrix} 3 \\ -4 \end{pmatrix} \\ \\&= \begin{pmatrix} -\frac{3}{2} + 2 \sqrt{3} \\ \frac{3}{2}\sqrt{3} + 2 \end{pmatrix} \end{aligned}$
Jadi, bayangan titik $X$ adalah $X''(-\frac{3}{2} + 2 \sqrt{3}, \frac{3}{2}\sqrt{3} + 2 )$
Contoh soal 4
Tentukanlah bayangan titik $Y(-6,-7)$ yang dirotasi $45^\circ$ searah dengan arah perputaran jarum jam dengan pusat putar $B(-3,5)$. Kemudian, dilanjutkan dengan rotasi $135^\circ$ dengan arah dan pusat yang sama.
Jawab:
Diketahui : Titik $Y(-6,-7)$ dirotasi sebesar $(\alpha+\beta)=45^\circ+135^\circ=180^\circ \rightarrow \color{red}{-180^\circ}$(karena searah dengan arah perputaran jarum jam) dengan pusat $B(-3,5)$
$\begin{aligned} \begin{pmatrix} x'' \\ y'' \end{pmatrix} &= \begin{pmatrix} cos\ (\alpha+\beta) & -sin\ (\alpha+\beta) \\ sin\ (\alpha+\beta) & cos \ (\alpha+\beta) \end{pmatrix}\begin{pmatrix} x - m \\ y - n\end{pmatrix} + \begin{pmatrix} m \\ n\end{pmatrix} \\ \\ &= \begin{pmatrix} cos\ (-180^\circ) & -sin\ (-180^\circ) \\ sin\ (-180^\circ) & cos \ (-180^\circ) \end{pmatrix}\begin{pmatrix} -6 - (-3) \\ -7 - 5\end{pmatrix} + \begin{pmatrix} -3 \\ 5\end{pmatrix} \\ \\ &= \begin{pmatrix} cos\ 180^\circ & sin\ 180^\circ \\ -sin\ 180^\circ & cos \ 180^\circ \end{pmatrix}\begin{pmatrix} -3 \\ -12 \end{pmatrix} + \begin{pmatrix} -3 \\ 5\end{pmatrix} \\ \\ &= \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix}\begin{pmatrix} -3 \\ -12 \end{pmatrix} + \begin{pmatrix} -3 \\ 5\end{pmatrix} \\ \\ &= \begin{pmatrix} 3 \\ 12 \end{pmatrix} + \begin{pmatrix} -3 \\ 5\end{pmatrix} \\ \\ &= \begin{pmatrix} 0 \\ 17 \end{pmatrix} \end{aligned}$
Jadi, bayangan titik $Y$ adalah $Y''(0,17)$
Contoh soal 5
Tentukanlah bayangan segitiga ABC dengan titik $A(5,0)$, $B(-10,0)$ dan $C(0,-15)$ yang dirotasi $225^\circ$ berlawanan dengan arah perputaran jarum jam dengan pusat putar $O(0,0)$.
Jawab:
Diketahui : Segitiga ABC dengan titik $A(5,0)$, $B(-10,0)$ dan $C(0,-15)$ dirotasi sebesar $\alpha=225^\circ$ dengan pusat $O(0,0)$
$\begin{aligned} \left( \begin{matrix} {x_1}' & {x_2}' & {x_3}' \\ {y_1}' & {y_2}' & {y_3}' \end{matrix} \right) & = \left(\begin{matrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{matrix} \right) \left( \begin{matrix} {x_1} & {x_2} & {x_3} \\ {y_1} & {y_2} & {y_3} \end{matrix} \right) \\ \\ & = \left(\begin{matrix} \cos 225^\circ & -\sin 225^\circ \\ \sin 225^\circ & \cos 225^\circ \end{matrix} \right) \left( \begin{matrix} 5 & -10 & 0 \\ 0 & 0 & -15 \end{matrix} \right) \\ \\ & = \left( \begin{matrix} -\frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \\ -\frac{1}{2}\sqrt{2} & -\frac{1}{2}\sqrt{2} \end{matrix} \right) \left( \begin{matrix} 5 & -10 & 0 \\ 0 & 0 & -15 \end{matrix} \right) \\ \\ & = \left( \begin{matrix} -\frac{5}{2}\sqrt{2} & 5\sqrt{2} & -\frac{15}{2}\sqrt{2} \\ -\frac{5}{2}\sqrt{2} & 5\sqrt{2} & \frac{15}{2}\sqrt{2} \end{matrix} \right) \end{aligned}$
Jadi, diperoleh bayangannya yaitu segitiga $A'B'C'$ dengan titik sudut $A'(-\frac{5}{2}\sqrt{2}, -\frac{5}{2}\sqrt{2})$, $B'(5\sqrt{2}, 5\sqrt{2})$, dan $C'(-\frac{15}{2}\sqrt{2}, \frac{15}{2}\sqrt{2})$
Contoh soal 6
Tentukanlah bayangan parabola $x^{2}+6y=0$ yang dirotasi $\frac{\pi}{3}$ berlawanan dengan arah perputaran jarum jam dengan pusat putar $C(4,2)$. Dilanjutkan dirotasi $\frac{\pi}{6}$ dengan pusat dan arah yang sama.
Jawab:
Diketahui :
Persamaan parabola : $x^{2}+6y=0$ dirotasi sebesar $(\alpha+\beta)= \frac{\pi}{3}+\frac{\pi}{6}=60^\circ+30^\circ=90^\circ$ dengan pusat $C(4,2)$
$\begin{aligned} \begin{pmatrix} x'' \\ y'' \end{pmatrix} &= \begin{pmatrix} cos\ (\alpha+\beta) & -sin\ (\alpha+\beta) \\ sin\ (\alpha+\beta) & cos \ (\alpha+\beta) \end{pmatrix}\begin{pmatrix} x - m \\ y - n\end{pmatrix} + \begin{pmatrix} m \\ n\end{pmatrix} \\ \\ &= \begin{pmatrix} cos\ 90 & -sin\ 90 \\ sin\ 90 & cos \ 90 \end{pmatrix}\begin{pmatrix} x - 4 \\ y - 2 \end{pmatrix} + \begin{pmatrix} 4 \\ 2 \end{pmatrix} \\ \\ &= \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}\begin{pmatrix} x-4 \\ y-2 \end{pmatrix} + \begin{pmatrix} 4 \\ 2 \end{pmatrix} \\ \\ &= \begin{pmatrix} -y+2 \\ x-4 \end{pmatrix} + \begin{pmatrix} 4 \\ 2 \end{pmatrix} \\ \\ &= \begin{pmatrix} -y+6 \\ x-2 \end{pmatrix} \end{aligned}$
Sehingga diperoleh
$x''=-y+6 \rightarrow y=6-x'' $
$y''=x-2 \rightarrow x=y''+2$
Substitusi nilai $x$ dan $y$ pada persamaan $x^{2}+6y=0$ sehingga diperoleh
$\begin{aligned} x^{2}+6y &= 0 \\ (y''+2)^{2}+6(6-x'') &= 0 \\ (y'')^{2}+4y''+4+36-6x'' &= 0 \\ (y'')^{2}+4y''-6x''+40 &= 0 \end{aligned}$
Jadi, bayangannya adalah $y^{2}+4y-6x+40=0$
Contoh soal 7
Bayangan titik $Z(x,y)$ yang dirotasi $270^\circ$ berlawanan dengan arah perputaran jarum jam dengan pusat $O(0,0)$ adalah $Z(-2,1)$. Tentukanlah nilai dari $x-y$
Jawab:
$\begin{aligned} \left( \begin{matrix} x' \\ y' \end{matrix} \right) & = \left(\begin{matrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{matrix} \right) \left( \begin{matrix} x \\ y \end{matrix} \right) \\ \\ \left( \begin{matrix} -2 \\ 1 \end{matrix} \right) & = \left( \begin{matrix} \cos 270^\circ & -\sin 270^\circ \\ \sin 270^\circ & \cos 270^\circ \end{matrix} \right) \left( \begin{matrix} x \\ y \end{matrix} \right) \\ \\ \left( \begin{matrix} -2 \\ 1 \end{matrix} \right) & = \left( \begin{matrix} 0 & 1 \\ -1 & 0 \end{matrix} \right) \left( \begin{matrix} x \\ y \end{matrix} \right) \\ \\ \left( \begin{matrix} -2 \\ 1 \end{matrix} \right) & = \left( \begin{matrix} y \\ -x \end{matrix} \right) \end{aligned}$
Sehingga diperoleh
$y=-2$
$x=-1$
Jadi, diperoleh titik $Z(-1,-2)$ sehingga nilai $x-y=-1+2=1$
Demikianlah beberapa contoh soal dan pembahasan pada materi transformasi rotasi. Semoga bermanfaat.
Referensi
E. S., Pesta dan Cecep Anwar H. F. S. 2008. Matematika aplikasi : untuk SMA dan MA kelas XII program studi ilmu alam. Jakarta: Pusat Perbukuan Departemen Pendidikan Nasional.
Kementerian Pendidikan dan Kebudayaan. 2014. Matematika untuk SMA/MA/SMK/MAK Kelas XI Semester 2. Jakarta: Kementerian Pendidikan dan Kebudayaan.