Contoh Soal Persamaan Kuadrat beserta Pembahasannya

Berikut ini mimin sajikan beberapa contoh soal dan pembahasan pada materi persamaan kuadrat. Selamat membaca, sobat. Semoga bermanfaat.
Contoh soal 1
Akar-akar persamaan kuadrat $x^2+ax-1=0$ adalah $p$ dan $q$. Jika $p^2-2pq+q^2=4a$ maka nilai $a$ adalah ...
Jawab:
Ingat sifat tambah dan kali akar-akar:
$\begin{aligned} &x^2+ax-1=0\\& p+q=-\frac{b}{a}=-\frac{a}{1}=-a\\& p \times q=\frac{c}{a}=\frac{-1}{1}=-1 \end{aligned}$
Mencari nilai $a$:
$\begin{aligned} p^2-2pq+q^2&=4a \\ (p+q)^2-4pq&=4a\\ (-a)^2-4(-1)&=4a \\ a^2-4a+4&=0\\(a-2)^2&=0\\a&=2 \end{aligned}$
Contoh soal 2
Persamaan kuadrat dari $x^2-2px-2p+3=0$ mempunyai dua akar yang sama. Nilai $p$ yang memenuhi adalah ...
Jawab:
Ingat $D=0$ untuk kedua akar sama, maka:
$\begin{aligned} b^2-4ac&=0\\ (-2p)^2-4(1)(-2p+3)&=0 \\ 4p^2+8p-12&=0\\ p^2+2p-3&=0\\ (p+3)(p-1)&=0 \\ p=-3 \vee p&=1 \end{aligned}$
Jadi, nilai $p$ yang memenuhi adalah $-3$ atau $1$
Contoh soal 3
Grafik $y=px^2+(p-4)x+p+1$ memotong sumbu $X$ di dua titik. Batas-batas nilai $p$ yang memenuhi adalah ...
Jawab:
Ingat $D>0$ grafik berpotongan di dua titik maka:
$\begin{aligned} b^2-4ac&>0\\ (p-4)^2-4(p)(p+1)&>0\\ p^2-8p+16-4p^2-4p&>0 \\ -3p^2-8p+16&>0\\ (-3p+4)(p+4)&>0 \end{aligned}$
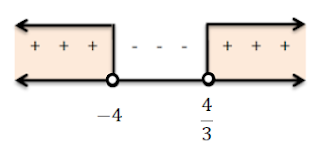
Jadi, batas-batas nilai $p$ yang memenuhi adalah $p<-4$ atau $p>\frac{4}{3}$
Contoh soal 4
Persamaan kuadrat $2x^2-2(p-4)+p=0$ mempunyai dua akar real berbeda. Batas-batas nilai $p$ yang memenuhi adalah ...
Jawab:
Ingat $D>0$ untuk kedua akar real berbeda, maka:
$\begin{aligned} b^2-4ac&>0\\ (-2p+8)^2-4(2)(p)&>0\\ 4p^2-32p+64-8p&>0 \\ 4p^2-40p+64&>0\\ p^2-10p+16&>0 \\ (p-8)(p-2)&>0 \end{aligned}$

Contoh soal 5
Jika $x_1$ dan $x_2$ adalah akar-akar persamaan $x^2-ax+b=0$ serta ${x_1}^2 x_2+x_1 {x_2}^2=30$ dan $\frac{1}{x_1}+\frac{1}{x_2}=\frac{6}{5}$ maka nilai $a^2-b^2$ adalah ...
Jawab:
${x_1}^2 x_2+x_1 {x_2}^2=30 \Rightarrow x_1 x_2(x_1 + x_2)=30$
$\frac{1}{x_1}+\frac{1}{x_2}=\frac{6}{5} \Rightarrow \frac{x_1+x_2}{x_1.x_2}=\frac{6}{5}$
Dari bentuk diatas diperoleh:
$x_1+x_2 =6$
$x_1.x_2=5$
Jadi, nilai $a^2-b^2=6^2-5^2=11$
Contoh soal 6
Persamaan kuadrat yang mempunyai akar $a$ dan $b$ sehingga $\frac{1}{a} + \frac{1}{b}=\frac{5}{6}$ adalah ...
Jawab:
Konstanta $a$ dan $b$ merupakan akar-akar suatu persamaan kuadrat
$\frac{1}{a} + \frac{1}{b}=\frac{5}{6} \Leftrightarrow \frac{(a+b)}{ab}=\frac{5}{6}$
Dari bentuk diatas diperoleh:
$a+b=5$
$a.b=6$
Menyusun persamaan kuadrat:
$x^2-(a+b)x+a.b=0$
$x^2-5x+6=0$
Contoh soal 7
Jika $(a,b)$ dengan $b \neq 2$ adalah penyelesaian dari sistem persamaan
$\begin{cases} &x^2-y^2-2x+4=0 \\&2xy-4xy=0 \end{cases}$
Maka $a+b=...$
Jawab:
Persamaan 1:
$\begin{aligned} &2xy-4y=0 \\ & \Leftrightarrow 2y(x-2)=0 \\ & \Leftrightarrow x=2 \vee y=0 \text{ (tidak memenuhi)} \end{aligned}$
Persamaan 2:
$\begin{aligned} &x^2-y^2-2x+4=0\\ & \Leftrightarrow 4-y^2-4+4=0 \\ & \Leftrightarrow 4-y^2=0 \\ & \Leftrightarrow y=2 \vee y=-2 \end{aligned}$
Penyelesaian dari sistem persamaan $(a,b)$ dengan $b \neq 2$ maka
$a=x=2$
$b=y=-2$
Jadi, nilai dari $a+b=2+(-2)=0$
Contoh soal 8
Akar-akar persamaan kuadrat $2x^2+bx+16=0$ adalah $p$ dan $q$. Jika $p=2q$ dan $p,q>0$, maka nilai $b$ adalah ...
Jawab:
$p=2q$ maka :
$p+q=-\frac{b}{a}=-\frac{b}{2} \Leftrightarrow 3q= -\frac{b}{2}$
$\begin{aligned} p.q=\frac{c}{a}=\frac{16}{2}=8 &\Leftrightarrow 2q.q=8 \\ &\Leftrightarrow q=\pm \sqrt{4}= \pm 2 \end{aligned}$
Syarat: $p,q>0$ maka $q=2$
$\begin{aligned} &3q=-\frac{b}{2}\\ &\Leftrightarrow 6 = -\frac{b}{2} \\ &\Leftrightarrow -b=12\\ &\Leftrightarrow b=-12 \end{aligned}$
Contoh soal 9
Persamaan kuadrat $(p-2)x^2-4px+2p-4=0$, mempunyai dua akar yang saling berkebalikan. Nilai $p$ yang memenuhi adalah ...
Jawab:
Akar-akar saling berkebalikan: $a=c$
$p-2=2p-4$
$2p-p=-2+4$
$p=2$
Contoh soal 10
Persamaan kuadrat $x^2+(p-2)x+2p-4=0$, tidak mempunyai akar-akar real. Batas-batas nilai $p$ yang memenuhi adalah ...
Jawab:
Tidak mempunyai akar-akar real : $D<0$
$D<0$
$\Leftrightarrow b^2-4ac<0 $
$\Leftrightarrow (p-2)^2-4.1.(2p-4)<0 $
$\Leftrightarrow p^2-4p+4-8p+16<0$
$\Leftrightarrow p^2-12p+10<0 $
$\Leftrightarrow (p-10)(p-2)<0$
$2<p<10$
Demikianlah beberapa contoh soal dan pembahasan pada materi persamaan kuadrat. Semoga bermanfaat.