Pembahasan Soal Buku Paket Matematika SMP/Mts Kelas 8 Semester 2 Halaman 22 (Kurikulum 2013)

Halo semuanya, pada postingan kali ini mimin akan sajikan pembahasan beberapa soal ayo kita berlatih 6.2 (buku paket matematika SMP/Mts kelas 8 halaman 22 semester 2 kurikulum 2013). Selamat belajar. Semoga bermanfaat.
Soal nomor 1
Tentukan jarak antara dua titik dari pasangan titik berikut
a). (10,20), (13,16)
b). (15,37), (42,73)
c). (-19,-16), (-2,14)
Jawab:
Untuk menghitung jarak antara dua titik dapat diselesaikan dengan menggunakan rumus:
$\text{Jarak}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$
Sehingga soal diatas dapat diselesaikan sebagai berikut
a). (10,20), (13,16)
Misal, (10,20) sebagai $(x_1,y_1)$ dan (13,16) sebagai $(x_2,y_2)$
$\begin{aligned} \text{Jarak}&=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ &=\sqrt{(13-10)^2+(16-20)^2} \\ &=\sqrt{(3)^2+(-4)^2}\\ &=\sqrt{9+16}\\ &=\sqrt{25}\\ &=5 \end{aligned}$
b). (15,37), (42,73)
Misal, (15,37) sebagai $(x_1,y_1)$ dan (42,73) sebagai $(x_2,y_2)$
$\begin{aligned} \text{Jarak}&=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ &=\sqrt{(42-15)^2+(73-37)^2} \\ &=\sqrt{(27)^2+(36)^2}\\ &=\sqrt{2025}\\ &=45 \end{aligned}$
c). (-19,-16), (-2,14)
Misal, (-19,-16) sebagai $(x_1,y_1)$ dan (-2,14) sebagai $(x_2,y_2)$
$\begin{aligned} \text{Jarak}&=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ &=\sqrt{(-2+19)^2+(14+16)^2} \\ &=\sqrt{(17)^2+(30)^2}\\ &=\sqrt{1189} \end{aligned}$
Soal nomor 2
Diketahui segitiga ABC dengan titik-titik A(-1,5), B(-1,1), dan C(2,1). Apakah segitiga ABC merupakan segitiga siku-siku? Jelaskan.
Jawab:
$\bullet$ Jarak titik AB
Misal, (-1,5) sebagai $(x_1,y_1)$ dan (-1,1) sebagai $(x_2,y_2)$
$\begin{aligned} \text{Jarak}&=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ &=\sqrt{(-1+1)^2+(1-5)^2} \\ &=\sqrt{(0)^2+(-4)^2}\\ &=\sqrt{16}\\ &=4 \end{aligned}$
$\bullet$ Jarak titik BC
Misal, (-1,1) sebagai $(x_1,y_1)$ dan (2,1) sebagai $(x_2,y_2)$
$\begin{aligned} \text{Jarak}&=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ &=\sqrt{(2+1)^2+(1-1)^2} \\ &=\sqrt{(3)^2+(0)^2}\\ &=\sqrt{9}\\ &=3 \end{aligned}$
$\bullet$ Jarak titik AC
Misal, (-1,5) sebagai $(x_1,y_1)$ dan (2,1) sebagai $(x_2,y_2)$
$\begin{aligned} \text{Jarak}&=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ &=\sqrt{(2+1)^2+(1-5)^2} \\ &=\sqrt{(3)^2+(-4)^2}\\ &=\sqrt{25}\\ &=5 \end{aligned}$
Pada segitiga siku-siku berlaku teorema phytagoras yaitu kuadrat sisi miring sama dengan jumlah kuadrat sisi siku-sikunya.
Sehingga, akan dibuktikan bahwa $AB^2+BC^2=AC^2$
$\begin{aligned} AB^2+BC^2&=AC^2\\ 4^2+3^2&=5^2 \\ 16+9&=25\\ 25 &= 25 \text{ (terbukti)} \end{aligned}$
Jadi, Segitiga ABC merupakan segitiga siku-siku karena panjang ketiga sisi segitiga memenuhi teorema Pythagoras, AB = 4 satuan, BC = 3 satuan, dan AC = 5 satuan
Berikut ini ilustrasi gambarnya

Soal nomor 3
Tentukan luas daerah yang diarsir dari setiap gambar berikut

Jawab:
a. Dari gambar pada poin a diatas dapat dilihat bahwa luas daerah yang diarsir merupakan luas setengah lingkaran. Sehingga luas daerah yang diarsir adalah sebagai berikut
$\begin{aligned} d^2&=20^2-16^2\\ d^2&=400-256\\ d&=\sqrt{144}\\ d&=12\\ \\ \text{Luas setengah lingkaran}&= \frac{1}{2} (\frac{1}{4} \pi d^2)\\ &= \frac{1}{8} \pi d^2\\ &= \frac{1}{8} \pi 12^2\\ &= 18 \pi \end{aligned}$
Jadi, luas daerah yang diarsir adalah $18 \pi~cm^2$
b. Dari gambar pada poin b diatas dapat dilihat bahwa luas daerah yang diarsir merupakan sebuah bangun trapesium. Sehingga luas daerah yang diarsir adalah sebagai berikut
$\begin{aligned} DC^2&=20^2-12^2\\ DC^2&=400-144\\ DC^2&=256\\ DC&=16\\ \\ AB^2&=20^2+15^2\\ AB^2&=400+225\\ AB^2&=625\\ AB&=25\\ \\ \text{Luas Trapesium}&= \frac{(DC+AB) \times 12}{2}\\ &=\frac{(16+25).12}{2}\\&=41 \times 6\\ &=246 \end{aligned}$
Jadi, luas daerah yang diarsir adalah $246~cm^2$
Soal nomor 4
Guru meminta kalian untuk menentukan jarak antara dua titik (4,2) dan (7,6). Kamu menggunakan (4,2) sebagai $(x_1,y_1)$ sedangkan temanmu menggunakan (7,6) sebagai $(x_1,y_1)$. Apakah kamu dan temanmu memperoleh hasil yang sama? Jelaskan.
Jawab:
Hasil jaraknya akan sama, meskipun kita gunakan (4,2) sebagai $(x_1,y_1)$ atau (7,6) sebagai $(x_1,y_1)$. Karena nilai jarak dari dua titik, hasilnya akan sama meskipun pemisalan titiknya dibalik.
Soal nomor 5
Ahmad dan Udin berdiri saling membelakangi untuk main tembak tembakan pistol bambu. Ahmad berjalan 20 langkah ke depan kemudian 15 langkah ke kanan. Pada saat yang sama, Udin berjalan 16 langkah ke depan kemudian 12 langkah ke kanan. Udin berhenti kemudian menembak Ahmad.
a. Gambar situasi di atas dengan menggunakan bidang Kartesius.
b. Berapa langkah jarak mereka berdua saat Udin menembak Ahmad
dengan pistol bambu?
Jawab:



Soal nomor 6
Seorang atlet tenis mengajukan pertanyaan kepada wasit. Suara atlet mampu didengar wasit hanya pada jarak maksimum 30 kaki. Berdasarkan posisi wasit dan atlet tenis pada gambar berikut, dapatkah wasit mendengar suara sang atlet? Jelaskan jawaban kalian.

Jawab:
Untuk mengetahui apakah suara atlet tenis terdengar oleh wasit maka haruslah diketahui jarak antara wasit dan atlet tenis. Berikut ini cara menghitung jaraknya

$\begin{aligned} x^2&=24^2+7^2\\ x^2&=576+49\\ x^2&=625\\ x&=\sqrt{625}\\ x&=25 \end{aligned}$
Dari penghitungan diatas dapat diperoleh bahwa jarak antara wasit dan atlet tenis adalah 25 kaki. Sehingga dapat disimpulkan bahwa wasit dapat mendengar suara atlet karena jarak antara wasit dan atlet tenis masih berjarak 25 kaki.
Soal nomor 7
Tinggi sebuah jendela lantai 2 pada sebuah gedung kira-kira 8 meter. Di depan gedung tersebut ada sebuah taman dengan lebar 6 m. Berapakah panjang tangga minimum yang dibutuhkan agar kaki-kaki tangga tidak merusak taman tersebut?
Jawab:
Ilustrasi dari soal diatas adalah sebagai berikut

$\begin{aligned} \text{tangga}&=\sqrt{8^2+6^2}\\ \text{tangga}&=\sqrt{100}\\ \text{tangga}&= 10 \end{aligned}$
Jadi, panjang minimum tangga adalah 10m
Soal nomor 8
Seorang penyelam dari Tim SAR mengaitkan dirinya pada tali sepanjang 25 m untuk mencari sisa-sisa bangkai pesawat di dasar laut. Laut diselami memiliki kedalaman 20 meter dan dasarnya rata. Berapakah luas daerah yang mampu dijangkau oleh penyelam tersebut?

Jawab:
Luas daerah yang mampu dijangkau oleh penyelam merupakan luas area sebuah lingkaran. Dimana jari-jarinya (r) dapat dihitung sebagai berikut
$\begin{aligned} r^2&=25^2-20^2\\ r^2&=625-400\\ r^2&=225\\ r&=\sqrt{225}\\ r&=15\\ \\L&=\pi r^2\\ &=\pi 15^2\\ &=225 \pi \end{aligned}$
Jadi, luas daerah yang mampu dijangkau oleh penyelam tersebut adalah $225 \pi ~m^2$ atau sekitar $706,5~m^2$
Soal nomor 9
Tentukan panjang AG dari bangun berikut.

Jawab:

Panjang AG adalah sebagai berikut
$\begin{aligned} EG^2&=EH^2+GH^2\\ EG^2&=10^2+10^2\\ EG^2&= 200\\ EG&=\sqrt{200} \\EG&= 10\sqrt{2}\\ \\ AG^2&= AE^2+EG^2\\ AG^2&= 10^2+(10\sqrt{2})^2\\ AG^2&= 300\\ AG&=\sqrt{300}\\ AG&=10\sqrt{3} \end{aligned}$Jadi, panjang AG adalah $10\sqrt{3}$

Panjang AG adalah sebagai berikut
$\begin{aligned} EG^2&=EH^2+GH^2\\ EG^2&=5^2+5^2\\ EG^2&= 50\\ EG&=\sqrt{50} \\EG&= 5\sqrt{2}\\ \\ AG^2&= AE^2+EG^2\\ AG^2&= 10^2+(5\sqrt{2})^2\\ AG^2&= 150\\ AG&=\sqrt{150}\\ AG&=5\sqrt{6} \end{aligned}$Jadi, panjang AG adalah $5\sqrt{6}$
Soal nomor 10
Bola A dan bola B digantung pada suatu kawat lurus seperti pada gambar di samping.
Diameter Bola A dan Bola B berturut-turut adalah 8 dan 18. Jika jarak ujung tali l dan n pada kawat adalah 5 dan panjang tali l adalah 10, berapakah panjang minimum tali n agar kedua tali bisa sejajar dan bola tidak saling menekan?
Jawab:
Ilustrasi dari soal diatas adalah sebagai berikut
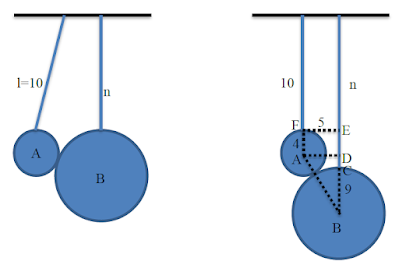
Panjang minimum tali n adalah sebagai berikut
$\begin{aligned} BD^2&=AB^2-AD^2\\ BD^2&=13^2-5^2\\ BD^2&=144\\ BD&=12\\ \\CD&=BD-9\\&=12-9\\&=3\\ \\n&=10+4+CD\\ &=14+3\\ &=17 \end{aligned}$
Jadi, panjang minimum tali n adalah 17 satuan panjang
Demikianlah pembahasan beberapa soal ayo kita berlatih 6.2 (buku paket matematika SMP/Mts kelas 8 halaman 22 semester 2 kurikulum 2013). Semoga bermanfaat.
Referensi
Kemdikbud. 2017. Matematika SMP/Mts Kelas VIII Semester 2 --Edisi Revisi. Jakarta: Kementerian Pendidikan dan Kebudayaan.