Catatan Materi, Contoh Soal dan Pembahasan Kedudukan Titik terhadap Lingkaran

Kedudukan Titik terhadap Lingkaran

$\bullet$ Jika jarak titik $P(x_1,y_1)$ ke pusat lingkaran kurang dari jari-jari lingkaran maka titik $P(x_1,y_1)$ berada di dalam lingkaran. Sehingga

$x_1^2 + y_1^2 < r^2$ ;

$(x_1 - a)^2 + (y_1 - b)^2 < r^2$ ;

$x_1^2 + y_1^2 + Ax_1 + By_1 + C < 0$.

$\bullet$ Jika jarak titik $P(x_1,y_1)$ ke pusat lingkaran sama dengan jari-jari lingkaran maka titik $P(x_1,y_1)$ berada pada lingkaran. Sehingga

$x_1^2 + y_1^2 = r^2$ ;

$(x_1 - a)^2 + (y_1 - b)^2 = r^2$ ;

$x_1^2 + y_1^2 + Ax_1 + By_1 + C = 0$.

$\bullet$ Jika jarak titik $P(x_1,y_1)$ ke pusat lingkaran lebih dari jari-jari lingkaran maka titik $P(x_1,y_1)$ berada di luar lingkaran. Sehingga

$x_1^2 + y_1^2 > r^2$ ;

$(x_1 - a)^2 + (y_1 - b)^2 > r^2$ ;

$x_1^2 + y_1^2 + Ax_1 + By_1 + C > 0$. 

Berikut ini beberapa contoh soal kedudukan titik terhadap lingkaran beserta pembahasannya.

Contoh soal 1

Tentukan posisi titik $A(8,3)$, $B(-3,-2)$, dan $C(1,7)$ terhadap lingkaran dengan persamaan $(x-2)^{2}+(y-3)^{2}=36$

Jawab:

Substitusikan koordinat titik-titik ke persamaan $(x-2)^{2}+(y-3)^{2}=36$ diperoleh :

Titik $A(8,3)$ terletak pada lingkaran sebab $(8-2)^{2}+(3-3)^{2}=36$

Titik $B(-3,-2)$ terletak di luar lingkaran sebab $(-3-2)^{2}+(-2-3)^{2}>36$

Titik $C(1,7)$ terletak di dalam lingkaran sebab $(1-2)^{2}+(7-3)^{2}<36$

Ilustrasinya sebagai berikut

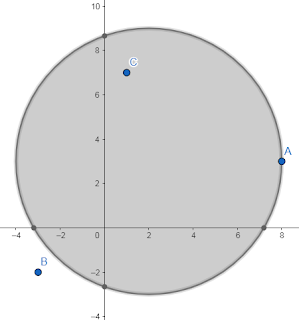
Contoh soal 2

Titik $Q(-4,3)$ terletak pada lingkaran $x^{2}+y^{2}-4x-py-23=0$. Tentukan nilai $p$

Jawab:

Titik $Q(-4,3)$ terletak pada lingkaran $x^{2}+y^{2}-4x-py-23=0$. Sehingga

$\begin{aligned} x^{2}+y^{2}-4x-py-23&=0 \\ (-4)^{2}+3^{2}-4(-4)-3p-23&=0 \\ 16+9+16-3p-23&=0 \\ 18-3p&=0 \\ 3p&=18 \\ p&=6  \end{aligned}$

Jadi, nilai $p=6$

Contoh soal 3

Titik $R(2,p)$ terletak di dalam lingkaran $x^{2}+y^{2}-4x+6y-12=0$. Tentukan nilai $p$ yang memenuhi.

Jawab:

Titik $R(2,p)$ terletak di dalam lingkaran $x^{2}+y^{2}-4x+6y-12=0$. Sehingga

$\begin{aligned} x^{2}+y^{2}-4x+6y-12&<0 \\ (2)^{2}+p^{2}-4.(2)+6p-12&<0 \\ 4+ p^{2}-8+6p-12&<0 \\ p^{2}+6p-16&<0 \\ (p+8)(p-2)&<0 \end{aligned}$

Jadi, nilai $p$ yang memenuhi adalah $-8<p<2$

Contoh soal 4

Titik $S(q,-3)$ terletak di luar lingkaran $x^{2}+y^{2}-4x+6y-12=0$. Tentukan nilai $q$ yang memenuhi.

Jawab:

Titik $S(q,-3)$ terletak di luar lingkaran $x^{2}+y^{2}-4x+6y-12=0$. Sehingga

$\begin{aligned} x^{2}+y^{2}-4x+6y-12&>0 \\ q^{2}+(-3)^{2}-4q+6(-3)-12&>0 \\ q^{2}+9-4q-18-12&>0 \\ q^{2}-4q-21&>0 \\ (q+3)(q-7)&>0 \end{aligned}$

Jadi, nilai $q$ yang memenuhi adalah $q<-3$ atau $q>7$

Demikianlah beberapa contoh soal dan pembahasan pada materi kedudukan titik terhadap lingkaran. Semoga bermanfaat. 

Referensi:

Djumanta, Wahyudin dan R. Sudrajat. 2008. Mahir Mengembangkan Matematika 2:untuk Kelas XI mengengah Atas / Madrasah Aliyah. Jakarta: Pusat Perbukuan Departemen Pendidikan Nasional.

Kementerian Pendidikan dan Kebudayaan. 2014. Matematika untuk SMA/MA/SMK/MAK Kelas XI Semester 2. Jakarta: Kementerian Pendidikan dan Kebudayaan.