Contoh Soal Transformasi Geometri - Translasi beserta Pembahasannya
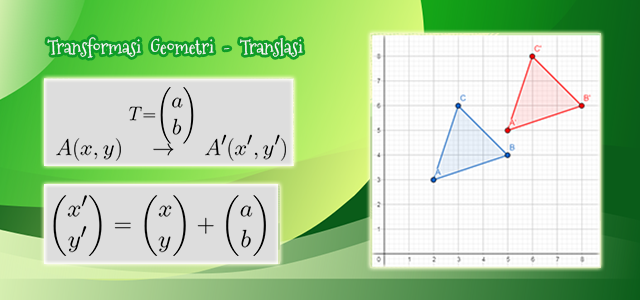
Translasi
Translasi (pergeseran) merupakan transformasi yang memindahkan titik pada bidang (objek) dengan arah dan jarak tertentu.
$\bullet$ Jika titik $A(x,y)$ ditranslasikan oleh $T = \left( \begin{matrix} a \\ b \end{matrix} \right)$, maka akan diperoleh $A'(x', y')$, secara notasi ditulis :
$A(x,y) \overset{T = \left( \begin{matrix} a \\ b \end{matrix} \right) }{ \huge \rightarrow} A' (x', y')$
$ \left( \begin{matrix} x' \\ y' \end{matrix} \right) = \left( \begin{matrix} x \\ y \end{matrix} \right) + \left( \begin{matrix} a \\ b \end{matrix} \right) $
$\bullet$ Jika titik $A(x,y)$ ditranslasikan oleh $T_1 = \left( \begin{matrix} a \\ b \end{matrix} \right)$ dilanjutkan dengan $T_2 = \left( \begin{matrix} c \\ d \end{matrix} \right)$ maka akan diperoleh $A''(x'', y'')$, secara notasi ditulis :
$A(x,y) \overset{T_2\ o\ T_1 = \begin{pmatrix} a + c \\ b + d\end{pmatrix} }{ \huge \rightarrow} A'' (x'', y'')$
$ \left( \begin{matrix} x'' \\ y'' \end{matrix} \right) = \left( \begin{matrix} x \\ y \end{matrix} \right) + \left( \begin{matrix} a+c \\ b+d \end{matrix} \right) $
Berikut ini beberapa contoh soal transformasi translasi dan pembahasannya.
Contoh soal 1
Translasi $T = \left( \begin{matrix} a \\ b \end{matrix} \right)$ memetakan titik $A(2,-6)$ ke $A'(-6,-3)$. Tentukan translasi tersebut.
Jawab:
$A(2,-6) \overset{T = \left( \begin{matrix} a \\ b \end{matrix} \right) }{ \huge \rightarrow} A' (-6, -3)$
$\begin{aligned} \left( \begin{matrix} x' \\ y' \end{matrix} \right) &= \left( \begin{matrix} x \\ y \end{matrix} \right) + \left( \begin{matrix} a \\ b \end{matrix} \right) \\ \left( \begin{matrix} -6 \\ -3 \end{matrix} \right) &= \left( \begin{matrix} 2 \\ -6 \end{matrix} \right) + \left( \begin{matrix} a \\ b \end{matrix} \right) \\ \left( \begin{matrix} a \\ b \end{matrix} \right) &= \left( \begin{matrix} -6 \\ -3 \end{matrix} \right) - \left( \begin{matrix} 2 \\ -6 \end{matrix} \right) \\ \left( \begin{matrix} a \\ b \end{matrix} \right) &= \left( \begin{matrix} -8 \\ 3 \end{matrix} \right) \end{aligned}$
Jadi, translasi tersebut adalah $T = \left( \begin{matrix} -8 \\ 3 \end{matrix} \right)$
Contoh soal 2
Tentukanlah bayangan segitiga ABC dengan titik sudut $A(2,3)$, $B(5,4)$, dan $C(3,6)$ oleh translasi $T = \left( \begin{matrix} 3 \\ 2 \end{matrix} \right)$.
Jawab:
$\begin{aligned} & A(2,3) \overset{T = \left( \begin{matrix} 3 \\ 2 \end{matrix} \right) }{ \huge \rightarrow} A' (x', y') \\ & B(5,4) {~\huge \rightarrow} ~~B' (x', y') \\ & C(3,6) {~\huge \rightarrow} ~~C' (x', y') \end{aligned}$
$\bullet ~A'$
$\begin{aligned} \left( \begin{matrix} x' \\ y' \end{matrix} \right) = \left( \begin{matrix} 2 \\ 3 \end{matrix} \right) + \left( \begin{matrix} 3 \\ 2 \end{matrix} \right) = \left( \begin{matrix} 5 \\ 5 \end{matrix} \right) \end{aligned}$
$\bullet ~B'$
$\begin{aligned} \left( \begin{matrix} x' \\ y' \end{matrix} \right) = \left( \begin{matrix} 5 \\ 4 \end{matrix} \right) + \left( \begin{matrix} 3 \\ 2 \end{matrix} \right) = \left( \begin{matrix} 8 \\ 6 \end{matrix} \right) \end{aligned}$
$\bullet ~C'$
$\begin{aligned} \left( \begin{matrix} x' \\ y' \end{matrix} \right) = \left( \begin{matrix} 3 \\ 6 \end{matrix} \right) + \left( \begin{matrix} 3 \\ 2 \end{matrix} \right) &= \left( \begin{matrix} 6 \\ 8 \end{matrix} \right) \end{aligned}$
Jadi, bayangan segitiga $ABC$ adalah segitiga $A'B'C'$ dengan titik $A'(5,5)$, $B'(8,6)$, dan $C'(6,8)$.
Contoh soal 3
Tentukanlah bayangan garis $3x+2y-3=0$ oleh translasi $T = \left( \begin{matrix} 1 \\ 2 \end{matrix} \right)$.
Jawab:
$\begin{aligned} \left( \begin{matrix} x' \\ y' \end{matrix} \right) &= \left( \begin{matrix} x \\ y \end{matrix} \right) + \left( \begin{matrix} a \\ b \end{matrix} \right) \\ \left( \begin{matrix} x' \\ y' \end{matrix} \right) &= \left( \begin{matrix} x \\ y \end{matrix} \right) + \left( \begin{matrix} 1 \\ 2 \end{matrix} \right) \\ \left( \begin{matrix} x \\ y \end{matrix} \right) &= \left( \begin{matrix} x' \\ y' \end{matrix} \right) - \left( \begin{matrix} 1 \\ 2 \end{matrix} \right) \end{aligned}$
Sehingga diperoleh
$\begin{aligned} x = x’-1 \\ y = y’-2 \end{aligned}$
Substitusi nilai $x$ dan $y$ pada persamaan garis $3x+2y-3=0$
$\begin{aligned} 3x+2y-3 & = 0 \\ 3(x'-1)+2(y'-2)-3 & = 0 \\ 3x'+2y'-3-4-3 & = 0 \\ 3x'+2y'-10 & = 0 \end{aligned}$
Jadi, bayangan garis $3x+2y-3=0$ oleh translasi $T = \left( \begin{matrix} 1 \\ 2 \end{matrix} \right)$ adalah $3x+2y-10 = 0$
Contoh soal 4
Tentukanlah bayangan lingkaran $x^{2}+y^{2}-4x-6=0$ yang ditranslasikan oleh $T_{2} = \left( \begin{matrix} 2 \\ -3 \end{matrix} \right)$ dilanjutkan oleh $T_{1} = \left( \begin{matrix} -1 \\ -1 \end{matrix} \right)$.
Jawab:
$A(x,y) \overset{T_2\ o\ T_1 = \begin{pmatrix} a + c \\ b + d\end{pmatrix} }{ \huge \rightarrow} A'' (x'', y'')$
$\begin{aligned} \left( \begin{matrix} x'' \\ y'' \end{matrix} \right) &= \left( \begin{matrix} x \\ y \end{matrix} \right) + \left( \begin{matrix} a +c \\ b+d \end{matrix} \right) \\ \left( \begin{matrix} x'' \\ y'' \end{matrix} \right) &= \left( \begin{matrix} x \\ y \end{matrix} \right) + \left( \begin{matrix} -1+2 \\ -1+(-3) \end{matrix} \right) \\ \left( \begin{matrix} x \\ y \end{matrix} \right) &= \left( \begin{matrix} x'' \\ y'' \end{matrix} \right) - \left( \begin{matrix} 1 \\ -4 \end{matrix} \right) \end{aligned}$
Sehingga diperoleh
$\begin{aligned} x = x''-1 \\ y = y''+4 \end{aligned}$
Substitusi nilai $x$ dan $y$ pada persamaan lingkaran $x^{2}+y^{2}-4x-6=0$
$\begin{aligned} x^{2}+y^{2}-4x-6 & = 0 \\ (x''-1)^{2}+(y''+4)^{2}-4(x''-1)-6 & = 0 \\ (x'')^{2}-2(x'')+1+(y'')^{2}+8(y'')+16-4(x'')+4-6 & = 0 \\ (x'')^{2}+(y'')^{2}-6(x'')+8(y'')+15 & = 0 \end{aligned}$
Jadi, bayangan lingkaran $x^{2}+y^{2}-4x-6=0$ yang ditranslasikan oleh $T_{2} = \left( \begin{matrix} 2 \\ -3 \end{matrix} \right)$ dilanjutkan oleh $T_{1} = \left( \begin{matrix} -1 \\ -1 \end{matrix} \right)$ adalah $x^{2}+y^{2}-6x+8y+15=0$
Contoh soal 5
Bayangan lingkaran $(x-2)^{2}+(y+3)^{2}=1$ oleh translasi $T = \left( \begin{matrix} a \\ b \end{matrix} \right)$ adalah $(x+3)^{2}+(y-1)^{2}=1$. Tentukan nilai $a+b$.
Jawab:
Diketahui :
Persamaan awal : $(x-2)^{2}+(y+3)^{2}=1$
Persamaan bayangan : $(x+3)^{2}+(y-1)^{2}=1$, bisa ditulis dengan $(x'+3)^{2}+(y'-1)^{2}=1$
$\begin{aligned} \left( \begin{matrix} x' \\ y' \end{matrix} \right) = \left( \begin{matrix} x \\ y \end{matrix} \right) + \left( \begin{matrix} a \\ b \end{matrix} \right) \end{aligned}$
Sehingga diperoleh
$\begin{aligned} x' = x+a \\ y' = y+b \end{aligned}$
Substitusi nilai $x'$ dan $y'$ ke persamaan bayangan $(x'+3)^{2}+(y'-1)^{2}=1$
$\begin{aligned} (x'+3)^{2}+(y'-1)^{2}&=1 \\ (x+a+3)^{2}+(y+b-1)^{2}&=1 \end{aligned}$
Bentuk persamaan $(x+a+3)^{2}+(y+b-1)^{2}=1$ adalah sama dengan bentuk persamaan awal $(x-2)^{2}+(y+3)^{2}=1$. Sehingga dapat diperoleh
$\begin{aligned} x+a+3 &= x-2 \\ a &= x-x-2-3 \\ a &= -5 \end{aligned}$
$\begin{aligned} y+b-1 &= y+3 \\ b &= y-y+3+1 \\ b &= 4 \end{aligned}$
Jadi, nilai $a+b=-5+4=-1$
Demikianlah beberapa contoh soal dan pembahasan pada materi translasi. Semoga bermanfaat.
Referensi
E. S., Pesta dan Cecep Anwar H. F. S. 2008. Matematika aplikasi : untuk SMA dan MA kelas XII program studi ilmu alam. Jakarta: Pusat Perbukuan Departemen Pendidikan Nasional.
Kementerian Pendidikan dan Kebudayaan. 2014. Matematika untuk SMA/MA/SMK/MAK Kelas XI Semester 2. Jakarta: Kementerian Pendidikan dan Kebudayaan.