Contoh Soal Suku Banyak SMA/MA beserta Pembahasannya
Pengertian Suku Banyak
Secara umum, suku banyak dalam peubah $x$ berderajat $n$ ditulis sebagai berikut.
$P(x)=a_{n}x^{n} + a_{n-1}x^{n-1}+ a_{n-2}x^{n-2}+ ... + a_{2}x^{2}+a_{1}x^{1}+a_{0}$
Dengan syarat: $n \in~$ bilangan cacah dan $a_{n}, a_{n-1}, ..., a_{0}$ disebut koefisien-koefisien suku banyak, $a_{0}$ disebut suku tetap dan $a_{n} \neq 0$
Contoh
$x^{4}+5x^{2}-4x+3$ adalah suku banyak berderajat $4$, dengan koefisien $x^{4}$ adalah $1$, koefisien $x^{2}$ adalah $5$, koefisien $x$ adalah $-4$, dan suku tetapnya adalah $3$.
$2x^{2}- \frac{7}{x} + 4$ adalah bukan suku banyak karena memuat pangkat negatif yaitu $\frac{7}{x}$ atau $7x^{-1}$ dengan pangkat $-1$ bukan anggota bilangan cacah.
Menentukan Nilai Suku Banyak
Untuk menentukan nilai suku banyak, dapat diperoleh dengan cara subtitusi ataupun dengan cara skema. Berikut ulasan contohnya.
Contoh Soal 1
Hitunglah nilai $f(x)=2x^{4}-x^{2}+8$ untuk $x=-3$
Jawab:
$\bullet$ Dengan cara substitusi
$\begin{aligned} f(x) &= 2x^{4}-x^{2}+8 \\ f(-3) &= 2(-3)^{4}-(-3)^{2}+8 \\ &= 2 \cdot 81 - 9 + 8 \\ &= 162 - 1 \\ &= 161 \end{aligned}$
Jadi, nilai suku banyak $f(x)$ untuk $x=-3$ adalah $161$
$\bullet$ Dengan cara skema/ horner
$\begin{array}{c|ccccc} \text{x = -3} & 2 & 0 & -1 & 0 & 8 \\ & \downarrow & -6 & 18 & -51 & 153 \\ \hline & 2 & -6 & 17 & -51 & \fbox{161} \end{array}$
Jadi, nilai suku banyak $f(x)$ untuk $x=-3$ adalah $161$
Contoh Soal 2
Tentukan nilai $p$ jika diketahui suku banyak $f(x)=3x^{5}+6x^{4}-px^{3}+10x-5$ dan $f(-2)=39$.
Jawab:
$\begin{array}{c|cccccc} \text{x = -2} & 3 & 6 & -p & 0 & 10 & -5 \\ & \downarrow & -6 & 0 & 2p & -4p & -20+8p \\ \hline & 3 & 0 & -p & 2p & 10 - 4p & \fbox{-25+8p} \end{array}$
Diperoleh $f(-2)=-25+8p$, sehingga
$\begin{aligned} f(-2) &= 39 \\ -25+8p &= 39 \\ 8p &= 64 \\ p &= 8 \end{aligned}$
Pembagian Suku Banyak
Pembagian suku banyak dapat dilakukan dengan dua cara yaitu dengan cara susun atau dengan cara horner.
Contoh Soal 3
Tentukanlah hasil bagi dan sisa pembagian dari $(x^{3}+2x^{2}+3x+6)$ dibagi $(x-2)$ dengan cara susun dan horner.
Jawab:
Dengan cara susun
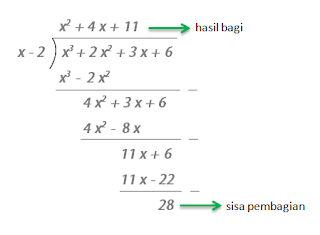
Dengan cara horner
Pembagian suku banyak $f(x)$ dibagi $(x-k)$ menghasilkan $h(x)$ sebagai hasil bagi dan $f(k)$ sebagai sisa pembagian, sedemikian hingga $f(x)=(x-k) \cdot h(x) + f(k)$.
Misalkan, suku banyak $ax^{3}+bx^{2}+cx+d$ dibagi oleh $(x-k)$. Penentuan nilai suku banyak dengan cara horner adalah sebagai berikut.
$\begin{array}{c|cccc} \text{x = k} & a & b & c & d \\ & \downarrow & ak & ak^{2}+bk & ak^{3}+bk^{2}+ck \\ \hline & \color{red}{a} & \color{red}{ak+b} & \color{red}{ak^{2}+bk+c} & \color{blue}{ak^{3}+bk^{2}+ck+d} \end{array}$
Dimana,
$a$, $ak+b$, dan $ak^{2}+bk+c $ merupakan koefisien hasil bagi berderajat dua
$ak^{3}+bk^{2}+ck+d$ merupakan sisa pembagian
Contoh soal nomor 3 diatas, jika diselesaikan dengan cara horner adalah sebagai berikut.
$\begin{array}{c|cccc} \text{x = 2} & 1 & 2 & 3 & 6 \\ & \downarrow & 2 & 8 & 22 \\ \hline & \color{red}{1} & \color{red}{4} & \color{red}{11} & \color{blue}{28} \end{array}$
Jadi, hasil bagi dari $(x^{3}+2x^{2}+3x+6)$ oleh $(x-2)$ adalah $x^{2}+4x+11$ dan sisanya adalah $28$
Pembagian Suku Banyak oleh Bentuk Linear $\color{green}{(ax + b)}$
Jika pada pembagian suku banyak $f(x)$ dibagi $\color{red}{(x-k)}$ menghasilkan $h(x)$ sebagai hasil bagi dan $f(k)$ sebagai sisa pembagian, sedemikian hingga $f(x)=(x-k) \cdot h(x) + f(k)$.
Pada pembagian suku banyak $f(x)$ dibagi $(ax+b)$, dapat diubah menjadi bentuk $f(x)$ dibagi $\color{red}{x-(-\frac{b}{a})}$, dalam hal ini berarti nilai $\color{red}{k= -\frac{b}{a}}$, sehingga pembagian suku banyak $f(x)$ dibagi $(ax+b)$ menghasilkan $\frac{h(x)}{a}$ sebagai hasil bagi dan $f(-\frac{b}{a})$ sebagai sisa pembagian, sedemikian hingga $f(x)=(ax+b) \cdot \frac{h(x)}{a} + f(-\frac{b}{a})$.
Contoh Soal 4
Tentukanlah hasil bagi dan sisa pembagian dari $(x^{3}-2x^{2}+4x-9)$ dibagi $(2x-1)$.
Jawab:
Karena pembaginya $(2x-1) = 2(x- \color{red}{\frac{1}{2}})$ maka faktor pengalinya adalah $\color{red}{x=\frac{1}{2}}$ sehingga penghitungan dengan cara horner-nya adalah sebagai berikut.
$\begin{array}{c|cccc} x = \frac{1}{2} & 1 & -2 & 4 & -9 \\ & \downarrow & \frac{1}{2} & -\frac{3}{4} & \frac{13}{8} \\ \hline & 1 & -\frac{3}{2} & \frac{13}{4} & -\frac{59}{8} \end{array}$
Jadi, hasil baginya adalah $ \frac{x^{2}-\frac{3}{2} x + \frac{13}{4}}{2} $ dan sisanya adalah $ -\frac{59}{8}$
Contoh Soal 5
Tentukanlah hasil bagi dan sisa pembagian dari $(x^{3}+7x^{2}+4)$ dibagi $(2x+1)$.
Jawab:
Karena pembaginya $(2x+1) = 2(x- \color{red}{(-\frac{1}{2})})$ maka faktor pengalinya adalah $\color{red}{x=-\frac{1}{2}}$ sehingga penghitungan dengan cara horner-nya adalah sebagai berikut.
$\begin{array}{c|cccc} x = -\frac{1}{2} & 1 & 7 & 0 & 4 \\ & \downarrow & -\frac{1}{2} & -\frac{13}{4} & \frac{13}{8} \\ \hline & 1 & \frac{13}{2} & -\frac{13}{4} & \frac{45}{8} \end{array}$
Jadi, hasil baginya adalah $ \frac{x^{2}+\frac{13}{2} x - \frac{13}{4}}{2} $ dan sisanya adalah $ \frac{45}{8}$
Pembagian Suku Banyak oleh Bentuk Kuadrat $\color{green}{(ax^{2} + bx+c)}$
Pembagian suku banyak dengan $ax^{2} + bx+c$, $a \neq 0$, dapat dilakukan dengan cara susun jika $ax^{2} + bx+c$ tidak dapat difaktorkan.
Adapun jika $ax^{2} + bx+c$ dapat difaktorkan, pembagian dapat dilakukan dengan cara susun ataupun dengan cara horner. Pembagian suku banyak $f(x)$ oleh $ax^{2} + bx+c$ dengan cara horner dimana $ax^{2} + bx+c$ dapat difaktorkan menjadi $(ax- k_{1})(x- k_{2})$ dapat ditulis sebagai berikut,
$ f(x)=(ax^{2}+bx+c) \cdot \color{blue}{\frac{h_{2}(x)}{a}} \color{red}{+} \left [ \color{red}{(ax-k_{1}) \cdot h_{1}(k_{2}) + f(\frac{k_{1}}{a})} \right ]$
dimana,
$(ax^{2}+bx+c)$ merupakan pembagi
$\frac{h_{2}(x)}{a}$ merupakan hasil bagi, dan
$(ax-k_{1}) \cdot h_{1}(k_{2}) + f(\frac{k_{1}}{a})$ merupakan sisa pembagian.
Untuk lebih jelasnya perhatikan contoh berikut.
Contoh Soal 6
Tentukanlah hasil bagi dan sisa pembagian dari $(x^{4}+4x^{3}+2x-5)$ dibagi $(x^{2}+2x-3)$.
Jawab:
Karena $(x^{2}+2x-3)$ dapat difaktorkan menjadi $(x-1)(x+3)$, maka pembagian dapat dilakukan dengan dua cara yaitu dengan cara horner ataupun dengan cara susun.
Dengan cara horner
$\begin{array}{c|cccc} x = 1 & 1 & 4 & 0 & 2 & -5 \\ & \downarrow & 1 & 5 & 5 & 7 \\ \hline x = -3 & 1 & 5 & 5 & 7 & \color{blue}{2} & \color{blue}{\Rightarrow f(\frac{k_{1}}{a})} \\ & \downarrow & -3 & -6 & 3 \\ \hline & \color{green}{1} & \color{green}{2} & \color{green}{-1} & \color{red}{10} & \color{red}{\Rightarrow h_{1}(k_{2})} \end{array}$
Dari skema horner diatas diperoleh,
$\color{green}{h_{2}(x) = x^{2} + 2x-1}$
$h_{1}(k_{2})=10$
$f(\frac{k_{1}}{a})=2$
Jadi, suku banyak $(x^{4}+4x^{3}+2x-5)$ dibagi $(x^{2}+2x-3)$ diperoleh,
Hasil baginya adalah $x^{2} + 2x-1$
Sisa pembagiannya adalah $(ax-k_{1}) \cdot h_{1}(k_{2}) + f(\frac{k_{1}}{a})= (x-1) \cdot 10 + 2 = \fbox{10x -8} $
Dengan cara susun

Teorema Faktor
Jika $f(x)$ suatu suku banyak, maka $(x-k)$ merupakan faktor dari $f(x)$ jika dan hanya jika $f(k)=0$
Contoh Soal 7
Tentukanlah faktor-faktor dari $P(x)=x^{3}-4x^{2}-x+4$
Jawab:
$P(x)$ berderajat 3 sehingga maksimum faktor berderajat satu yang diperoleh adalah 3 buah. Jika $(x-k)$ merupakan faktor dari $P(x)=x^{3}-4x^{2}-x+4$ maka nilai $k$ yang diperoleh adalah pembagi bulat dari $4$, yaitu $\pm 1$, $\pm 2$, dan $\pm 4$. Nilai-nilai $k$ tersebut disubtitusikan pada $P(x)$.
- Untuk $k= -1 \Rightarrow P(-1)=(-1)^{3}-4(-1)^{2}-(-1)+4=0$
$P(x) = 0$ maka $(x+1)$ faktor dari $P(x)$
- Untuk $k= 1 \Rightarrow P(1)=(1)^{3}-4(1)^{2}-(1)+4=0$
$P(x) = 0$ maka $(x-1)$ faktor dari $P(x)$
- Untuk $k= -2 \Rightarrow P(-2)=(-2)^{3}-4(-2)^{2}-(-2)+4=-10$
$P(x) \neq 0$ maka $(x+2)$ bukan faktor dari $P(x)$
- Untuk $k= 2 \Rightarrow P(2)=(2)^{3}-4(2)^{2}-(2)+4=-6$
$P(x) \neq 0$ maka $(x-2)$ bukan faktor dari $P(x)$
- Untuk $k= -4 \Rightarrow P(-4)=(-4)^{3}-4(-4)^{2}-(-4)+4=8$
$P(x) \neq 0$ maka $(x+4)$ bukan faktor dari $P(x)$
- Untuk $k= 4 \Rightarrow P(4)=(4)^{3}-4(4)^{2}-(4)+4=0 $
$P(x) = 0$ maka $(x-4)$ faktor dari $P(x)$
Jadi, $(x+1)$, $(x-1)$, dan $(x-4)$ adalah faktor-faktor dari $P(x)=x^{3}-4x^{2}-x+4$
Contoh Soal 8
Jika $x+1$ merupakan faktor suku banyak $x^{3}-3x^{2}-x+p$. Tentukanlah faktor-faktor lainnya.
Jawab:
Karena $x+1$ adalah faktor dari $x^{3}-3x^{2}-x+p$ maka
untuk $x=-1$ bisa diperoleh $x^{3}-3x^{2}-x+p=0$
$\begin{aligned} (-1)^{3}-3(-1)^{2}-(-1)+p &= 0 \\ -3+p &= 0 \\ p &= 3 \end{aligned}$
Jadi, bentuk suku banyaknya adalah $f(x)=x^{3}-3x^{2}-x+3$
$\begin{array}{c|cccc} x = -1 & 1 & -3 & -1 & 3 \\ & \downarrow & -1 & 4 & -3 \\ \hline x = 1 & 1 & -4 & 3 & \fbox{0} \\ & \downarrow & 1 & -3 \\ \hline x=3 & 1 & -3 & \fbox{0} \\ & \downarrow & 3 \\ \hline & 1 & \fbox{0} \end{array}$
Jadi, faktor-faktor yang lain adalah $(x-1)$ dan $(x-3)$
Demikianlah beberapa contoh soal dan pembahasan pada materi suku banyak. Semoga bermanfaat.
Referensi
Djumanta, Wahyudin dan R. Sudrajat. 2008. Mahir Mengembangkan Matematika 2:untuk Kelas XI mengengah Atas / Madrasah Aliyah. Jakarta: Pusat Perbukuan Departemen Pendidikan Nasional.
Soedyarto, Nugroho dan Maryanto. 2008. Matematika 2 untuk SMA atau MA Kelas XI Program IPA. Jakarta: Pusat Perbukuan Departemen Pendidikan Nasional.